|
Obsah
« 3. Přesnost měření 4. Některá rozdělení náhodných veličin Úvod
Kromě charakteristik náhodných veličin je nejúplnější charakteristikou tzv. rozdělení pravděpodobnosti náhodné veličiny, které je udáno vzorcem, grafem, či tabulkou. Uvedeme zde v naší disciplíně nejpoužívanější rozdělení, jak pro diskrétní, tak pro spojité náhodné proměnné a to binomické rozdělení a normální rozdělení. Dále v řadě matematicko - statistických úloh mají zvláštní význam tři rozdělení, která jsou odvozena z normálního rozdělení. Jsou to rozdělení Binomické rozdělení
Pro diskrétní náhodnou proměnnou používáme v grafickém vyjádření nejčastěji sloupcovitý graf, zvaný histogram a typickým rozdělením je tzv. binomické rozdělení použitelné při opakovaném pokusu (či měření téže veličiny) za stejných podmínek. Náhodnou veličinou je zde počet výskytů Pravděpodobnost je dána vztahem
kde jsme označili pravděpodobnost zkoumaného jevu
Základními charakteristikami binomického rozdělení jsou:
Normální rozdělení (Laplace - Gaussovo)
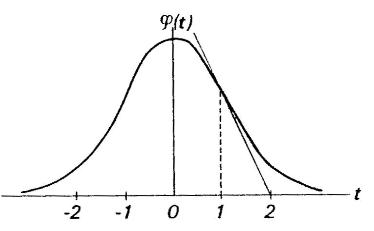
Toto rozdělení je nejdůležitějším rozdělením spojité náhodné veličiny, kterým lze za jistých podmínek aproximovat i některá rozdělení diskrétní. Obecně lze říci, že toto rozdělení je použitelné všude tam, kde kolísání náhodné veličiny je způsobeno součtem velkého počtu nepatrných a vzájemně nezávislých vlivů. Matematickým odvozením normálního rozdělení se nebudeme zabývat, velmi názorně však ilustruje vznik normálního rozdělení případ binomického rozdělení s pravděpodobnostmi Hustota pravděpodobnosti normálního rozdělení je dána frekvenční funkcí, jejíž graf je znám pod názvem „Gaussova křivka“:
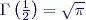
Tato frekvenční funkce má dva parametry a to střední hodnotu
Z dalších charakteristik uvedeme momenty
Uvedeme zde také normovanou veličinu
Tato veličina má normované normální rozdělení
a distribuční funkce
Obr. 1 Normální rozdělení Obě funkce se tabelují a tyto tabulky se používají i pro stanovení hodnot hustoty pravděpodobnosti i distribuční funkce nenormovaného normálního rozdělení.
Při praktických aplikacích se při výpočtech vždy nejdříve přechází z náhodné veličiny
V praxi se často využívá symetrie frekvenční funkce normálního rozdělení a tabeluje se místo distribuční funkce tzv. Laplaceova funkce (pro
pro kterou platí následující relace:
Pro stanovení pravděpodobnosti, že náhodná veličina s rozdělením
Hledaná pravděpodobnost pak bude:
Rozdělení Chí-kvadrát
Uvažujme
těchto veličin má tzv.
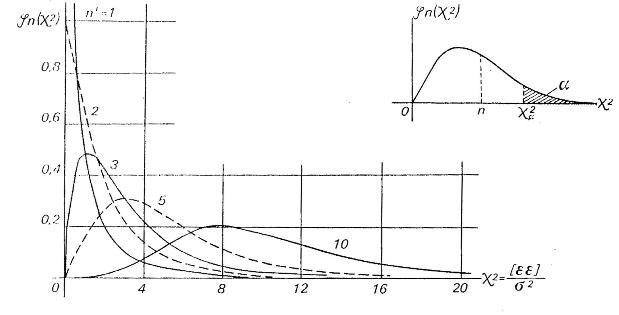
Obr. 2
Parametr
Pro celá
Např. platí
a bývá tabelována pro různé počty stupňů volnosti
Studentovo t-rozdělení
Mějme dvě nezávislé veličiny
bude
Distribuční funkce bude:
Obr. 3 Studentovo
Rozdělení s hustotou pravděpodobnosti
Rozdělení t je symetrické s jedním vrcholem v bodě
Při tabelaci kritických hodnot pouze pro Rozdělení F (Snedecorovo - Fisherovo)
Mějme dvě nezávislé veličiny
má Snedecorovo (Fisherovo)
Distribuční funkce bude
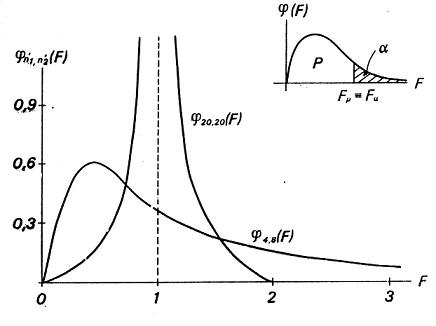
Obr. 4 Snedecorovo - Fisherovo
Rozdělení s hustotou pravděpodobnosti
V případě tabelace kritických hodnot pouze pro hodnoty |
 (čteme chí-kvadrát), Studentovo
(čteme chí-kvadrát), Studentovo  -rozdělení a Snedecorovo - Fischerovo
-rozdělení a Snedecorovo - Fischerovo  -rozdělení.
-rozdělení.
 určitého jevu
určitého jevu  (počet chyb stejného znaménka) při provedení
(počet chyb stejného znaménka) při provedení  opakování.
opakování.
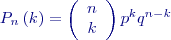 pro
pro  ,
,
 a opačnou pravděpodobnost (pravděpodobnost, že zkoumaný jev nenastane)
a opačnou pravděpodobnost (pravděpodobnost, že zkoumaný jev nenastane) 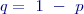 . Tento vztah se též nazývá frekvenční funkcí a pravděpodobnost, že se náhodná proměnná uskuteční až do konkrétního počtu
. Tento vztah se též nazývá frekvenční funkcí a pravděpodobnost, že se náhodná proměnná uskuteční až do konkrétního počtu 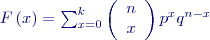 pro
pro  .
.

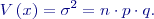
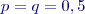 (pravděpodobnost výskytu kladné a záporné chyby) a s rostoucím
(pravděpodobnost výskytu kladné a záporné chyby) a s rostoucím  .
.
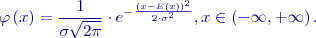
 (může být libovolná) a varianci
(může být libovolná) a varianci  . Normální rozdělení značíme
. Normální rozdělení značíme  . Frekvenční funkce má vrchol v bodě
. Frekvenční funkce má vrchol v bodě  . Distribuční funkce normálního rozdělení bude
. Distribuční funkce normálního rozdělení bude
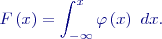




 , protože platí relace
, protože platí relace  ,
,  . Hustota pravděpodobnosti veličiny
. Hustota pravděpodobnosti veličiny 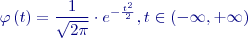
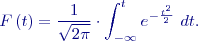
 a
a  a přejde se zpět na veličinu
a přejde se zpět na veličinu  se odvozují ze vztahů
se odvozují ze vztahů

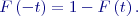
 )
)
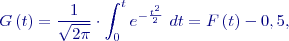
 ;
;  ;
;  ;
; 
 .
.
 nabude hodnoty z nějakého intervalu
nabude hodnoty z nějakého intervalu  postupujeme tak, že stanovíme dolní mez normované veličiny
postupujeme tak, že stanovíme dolní mez normované veličiny  , stanovíme dolní mez normované veličiny
, stanovíme dolní mez normované veličiny  :
:
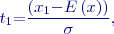
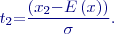
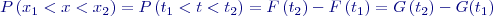
 náhodných veličin
náhodných veličin  ,
,  , …,
, …,  , které jsou vzájemně nezávislé a každá z nich má normální rozdělení
, které jsou vzájemně nezávislé a každá z nich má normální rozdělení  . Potom rozdělení součtu čtverců
. Potom rozdělení součtu čtverců
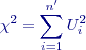
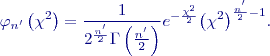

 rozdělení
rozdělení
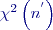 . Funkce
. Funkce  (Eulerův integrál) je pro
(Eulerův integrál) je pro  definována:
definována:
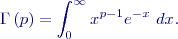

 . Střední hodnota bude:
. Střední hodnota bude: 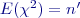 a variance
a variance  . Distribuční funkce bude
. Distribuční funkce bude
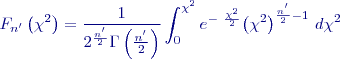
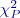 , tj. hodnoty, které splňují pro dané
, tj. hodnoty, které splňují pro dané 
 , tj. hodnoty, které splňují pro dané
, tj. hodnoty, které splňují pro dané 
 nazýváme hladinou významnosti či rizikem.
nazýváme hladinou významnosti či rizikem.
 a
a  . Potom hustota pravděpodobnosti veličiny
. Potom hustota pravděpodobnosti veličiny
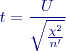
 , pro
, pro  a
a 

 se nazývá Studentovo
se nazývá Studentovo  . Počet stupňů volnosti je dán počtem stupňů volnosti veličiny ve jmenovateli veličiny
. Počet stupňů volnosti je dán počtem stupňů volnosti veličiny ve jmenovateli veličiny  . Pro
. Pro  lze velmi dobře Studentovo
lze velmi dobře Studentovo  ,
, pro argument
pro argument  ,
,  pro argument
pro argument  se kritické hodnoty pro
se kritické hodnoty pro  stanoví ze vztahu
stanoví ze vztahu  , což současně platí i pro kvantily
, což současně platí i pro kvantily  a
a  . Veličina
. Veličina  a veličina
a veličina  . Potom veličina
. Potom veličina
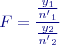
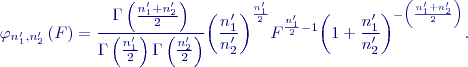

 se nazývá Snedecorovo
se nazývá Snedecorovo  ,
,  stupni volnosti a značí se
stupni volnosti a značí se  . Přitom
. Přitom  , (
, ( ) v čitateli (jmenovateli) náhodné veličiny
) v čitateli (jmenovateli) náhodné veličiny  pro argument
pro argument  pro argument
pro argument  , použijeme pro výpočet hodnot pro
, použijeme pro výpočet hodnot pro  vztah
vztah  , což znamená, že za
, což znamená, že za  procentní kritickou hodnotu rozdělení
procentní kritickou hodnotu rozdělení  procentní kritické hodnoty rozdělení
procentní kritické hodnoty rozdělení  , tedy z rozdělení se zaměněnými počty stupňů volnosti.
, tedy z rozdělení se zaměněnými počty stupňů volnosti.