|
Obsah
« 6. Vícerozměrná náhodná veličina 7. Chyby dvojrozměrné Úvod
Přejdeme nyní k případu, kdy rozptylový obrazec je plošný. Jako příklad zvolme střelbu z děla na cíl
K určení tvaru dvojrozměrného rozdělení musíme uvažovat plošný element rozptylové roviny. K tomu zvolíme osy souřadnic
U plošných chyb neexistuji kladné a záporné chyby.
Pravděpodobnostní element, že chyba
kde funkci Obr. 1 Elipsa chyb Elipsa chyb
Předpokládejme, že chyby
Vyjádřením veličiny
Body stejné sdružené hustoty pravděpodobnosti
které se nazývají elipsy chyb stejné hustoty pravděpodobnosti, zkráceně elipsy chyb (Obr. 1). Volbou proměnné
 , ,  , ,
čímž vynikne podstata proměnné
Na obvodě elipsy chyb leží nyní polohové chyby
Po obvodě kružnice chyb stejné velikosti (
Sdružená hustota pravděpodobnosti
K lepšímu osvětlení nalezených zákonů podáme geometrický názorný příklad. Kdybychom vystřelili dostatečný počet
Po zavedení proměnné
což je sdružená hustota pravděpodobnosti, platící po celém obvodě elipsy, která přísluší parametru Další definice:
nebo
podle toho, půjde-li o skutečné chyby nebo opravy k aritmetickým průměrům. V případě
s názvem „střední chyba souřadnicová“. Je to přibližně střední vzdálenost bodů na obvodě střední elipsy chyb od centra (bezchybné nebo vyrovnané polohy). Kružnice chybV případě stejné přesnosti měření v obou osách
přejdou elipsy chyb v kružnice chyb o poloměru
tabelované hodnoty i grafy funkce Stočené soustavy chybových souřadnic x, y
V předešlém případě osy souřadnic Obr. 2 Stočená soustava chybových souřadnicových os
Eventuální systematický posun těžiště chyb
Stočení os u elips chyb vzhledem k užitým osám chybových souřadnic
Označme původní odměřené souřadnice chybových bodů
(s kontrolou
Vytvoříme součty čtverců souřadnic nové soustavy
Úhel
Stejnou rovnici dá derivace
Úhel
Z redukovaných souřadnic (
Ve jmenovateli je
Pravděpodobnostní element pro chybu v poloze
Střední elipsa chyb má poloosy Elipsa chyb v případě vyrovnání zprostředkujících měření
Při vyrovnání zprostředkujících měření se v geodetické praxi často vyskytují případy, že v rovnicích oprav
Nejsou-li souřadnice
Nejen v triangulaci však nastává obecně, že hlavní osy elips chyb
Po dosazení za
Velikosti hlavních poloos jsou dány vztahy
Odvození stočení chybových os a jejich velikosti lze snadno odvodit z kovarianční matice pomocí jejích vlastních čísel. Koncové body úseček
« 6. Vícerozměrná náhodná veličina |
 (
(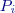 bude příslušet chyba
bude příslušet chyba  ; tato spojnice dává směr i velikost chyby. Také zde bude platit Gaussův zákon o větší četnosti malých chyb. Chyby se však nyní rozptylují na ploše ohraničené obvodem největších nevyhnutelných chyb, jaké můžeme připustit.
; tato spojnice dává směr i velikost chyby. Také zde bude platit Gaussův zákon o větší četnosti malých chyb. Chyby se však nyní rozptylují na ploše ohraničené obvodem největších nevyhnutelných chyb, jaké můžeme připustit.
 ,
,  v podélném a příčném směru s počátkem v cíli
v podélném a příčném směru s počátkem v cíli  bude výsledná chyba, vzniklá střetnutím dvou vzájemně nezávislých chyb v podélném a příčném směru
bude výsledná chyba, vzniklá střetnutím dvou vzájemně nezávislých chyb v podélném a příčném směru 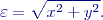
 .
. bude v mezích
bude v mezích  je
je  a že bude v mezích
a že bude v mezích  je
je  . Dvojrozměrný pravděpodobnostní element, že chyba
. Dvojrozměrný pravděpodobnostní element, že chyba  se souřadnicemi rohu
se souřadnicemi rohu 
 nazýváme sdruženou hustotou pravděpodobnosti. Chyby
nazýváme sdruženou hustotou pravděpodobnosti. Chyby 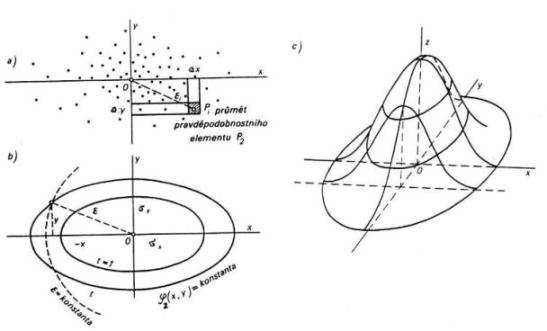
 ,
, 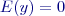 a že variance obou proměnných nejsou stejné:
a že variance obou proměnných nejsou stejné:

 dostaneme pravděpodobnostní element v soustavě dvou náhodných, normálně rozdělených veličin, které jsou vzájemně nezávislé
dostaneme pravděpodobnostní element v soustavě dvou náhodných, normálně rozdělených veličin, které jsou vzájemně nezávislé

 budou nyní tvořit soustavu soustředných a souosých elips, daných rovnicemi
budou nyní tvořit soustavu soustředných a souosých elips, daných rovnicemi
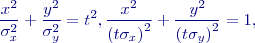
 definujeme hustotu pravděpodobnosti na elipse chyb; přitom střední souřadnicové chyby
definujeme hustotu pravděpodobnosti na elipse chyb; přitom střední souřadnicové chyby  ,
,  jsou konstantní pro soubor elips náležející určitému souboru chyb. Osový tvar elips chyb je
jsou konstantní pro soubor elips náležející určitému souboru chyb. Osový tvar elips chyb je
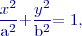
 ve zvoleném případě leží na osách
ve zvoleném případě leží na osách  , které mají stejnou sdruženou hustotu pravděpodobnosti
, které mají stejnou sdruženou hustotu pravděpodobnosti  ). Extrémní velikosti padnou právě do směru souřadnicových os
). Extrémní velikosti padnou právě do směru souřadnicových os  ) by se opět měnila sdružená hustota pravděpodobnosti
) by se opět měnila sdružená hustota pravděpodobnosti  ; extrémní hustoty jsou opět v průsečících kružnice s osami pravděpodobností
; extrémní hustoty jsou opět v průsečících kružnice s osami pravděpodobností  plošných elementů bude proměnlivá s místem, maximální v cíli
plošných elementů bude proměnlivá s místem, maximální v cíli  ) a klesající s rostoucí hodnotou proměnné
) a klesající s rostoucí hodnotou proměnné  , dají zvonovité těleso, k němuž je rovina
, dají zvonovité těleso, k němuž je rovina 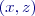 , kdy
, kdy  , dají soubor vzájemně podobných Gaussových křivek
, dají soubor vzájemně podobných Gaussových křivek  , kde
, kde  se mění se vzdáleností
se mění se vzdáleností  , kde
, kde  , dají opět soubor podobných Gaussových křivek
, dají opět soubor podobných Gaussových křivek  , jejich tvar však bude odlišný od tvaru křivek prvního souboru. Gaussova křivka vzniká i v libovolném řezu, pokud obsahuje osu
, jejich tvar však bude odlišný od tvaru křivek prvního souboru. Gaussova křivka vzniká i v libovolném řezu, pokud obsahuje osu  .
.
 plastických střel, které se přilepí na terč, vytvoří se (při normálním rozdělení chyb ve směrech obou souřadnicových os) uvedené zvonovité těleso. Kdybychom po střelbě odstranili cíl, pak podle MNČ (metody nejmenších čtverců) odhadneme jeho nejpravděpodobnější polohu v těžišti zásahů.
plastických střel, které se přilepí na terč, vytvoří se (při normálním rozdělení chyb ve směrech obou souřadnicových os) uvedené zvonovité těleso. Kdybychom po střelbě odstranili cíl, pak podle MNČ (metody nejmenších čtverců) odhadneme jeho nejpravděpodobnější polohu v těžišti zásahů.
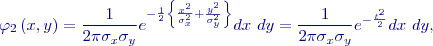
 ,
,  . Hodnoty
. Hodnoty  , má hlavní poloosy rovné středním souřadnicovým chybám
, má hlavní poloosy rovné středním souřadnicovým chybám  ,
,  a nazývá se střední elipsa chyb.
a nazývá se střední elipsa chyb.
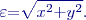



 je
je  . Proto jako kritérium přesnosti polohy bodu je vhodnější volit
. Proto jako kritérium přesnosti polohy bodu je vhodnější volit
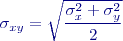

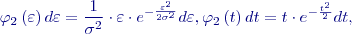
 jsou shodné jako u elipsy chyb. Střední elipsa chyb se v tomto případě nazývá „střední kružnice chyb“.
jsou shodné jako u elipsy chyb. Střední elipsa chyb se v tomto případě nazývá „střední kružnice chyb“.
 ,
,  nesplývají s naší soustavou souřadnic
nesplývají s naší soustavou souřadnic 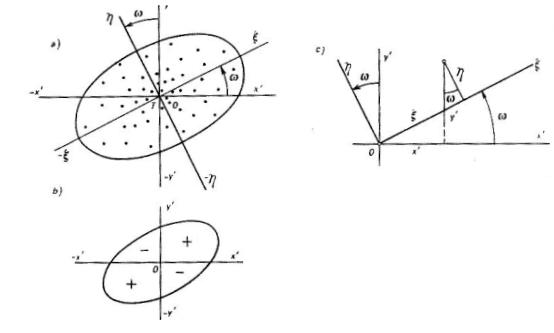
 vzhledem k počátku
vzhledem k počátku ![Equation $$
x_T=\frac{\left[x\right]}{n}\ ,\ y_T=\frac{\left[y\right]}{n}.
$$](/wiki/lib/exe/fetch.php?media=wiki:latex:/imgf3df127c1f6a1d2fc373811887805cc9.png)
![Math $[x_iy_i]$](/wiki/lib/exe/fetch.php?media=wiki:latex:/img970a7fd835ff831749ee347efe80f225.png) , která v nestočené poloze a gaussovském souboru má dávat
, která v nestočené poloze a gaussovském souboru má dávat  a hodnoty extrémních středních chyb
a hodnoty extrémních středních chyb  ,
,  ve směru os pravděpodobností.
ve směru os pravděpodobností.
![Equation $$
{x'}_i=x_i-\frac{\left[x\right]}{n}\ ,\ {y'}_i=y_i-\frac{\left[y\right]}{n},
$$](/wiki/lib/exe/fetch.php?media=wiki:latex:/img0d252cb652c1c505b12d5b339f440fff.png)
![Math $[x']=0$](/wiki/lib/exe/fetch.php?media=wiki:latex:/imgd0cd7b5fbf4e1d643a95d7217eeddbc3.png) ,
, ![Math $[y']=0$](/wiki/lib/exe/fetch.php?media=wiki:latex:/img14dd77251859e2553f83e353ba5748b3.png) ) posuneme počátek
) posuneme počátek  do těžiště
do těžiště ![Equation $$
\xi {\rm =}x{{\rm '}}\cdot {\cos \left(\omega \right)\ }{\rm +}y{{\rm '}}\cdot {\sin \left(\omega \right)\ }{\rm ,\ \ }\left[\xi \right]{\rm =0},
$$](/wiki/lib/exe/fetch.php?media=wiki:latex:/imgae1d7ff18d53911cce0fd2ce9166af6b.png)
![Equation $$
\eta =x{{\rm '}}\cdot {\sin \left(\omega \right)\ }{\rm -}y{{\rm '}}\cdot {\cos \left(\omega \right)\ }{\rm ,\ \ }\left[\eta \right]{\rm =0}.
$$](/wiki/lib/exe/fetch.php?media=wiki:latex:/img0bd94d7cde18fa4a516ebb64419c2e34.png)
![Equation $$
\left[\xi \xi \right]{\rm =}\left[x{{\rm '}}x{{\rm '}}\right]\cdot {{\cos }^2 \left(\omega \right)\ }{\rm +}\left[x{{\rm '}}y{{\rm '}}\right]\cdot {\sin \left({\rm 2}\omega \right)\ }+\left[{{\rm y}}{{\rm '}}{{\rm y}}{{\rm '}}\right]\cdot {{\sin }^2 \left(\omega \right)\ },
$$](/wiki/lib/exe/fetch.php?media=wiki:latex:/img45ef76944ed99ccc7bec63b384767e70.png)
![Equation $$
\left[\eta \eta \right]{\rm =}\left[x{{\rm '}}x{{\rm '}}\right]\cdot {{\sin }^2 \left(\omega \right)\ }{\rm -}\left[x{{\rm '}}y{{\rm '}}\right]\cdot {\sin \left({\rm 2}\omega \right)\ }+\left[{{\rm y}}{{\rm '}}{{\rm y}}{{\rm '}}\right]\cdot {{\cos }^2 \left(\omega \right)\ }.
$$](/wiki/lib/exe/fetch.php?media=wiki:latex:/imgcacb71e3558dd5ba48048cfa44abc8dd.png)
![Math $[\xi \xi ]$](/wiki/lib/exe/fetch.php?media=wiki:latex:/imgccaabd6072b8b9e075f7e34fa5058598.png) a
a ![Math $[\eta \eta ]$](/wiki/lib/exe/fetch.php?media=wiki:latex:/img1b52a0c3c78e185630a221d2402acb62.png) měly extrémní hodnotu. Položíme derivaci
měly extrémní hodnotu. Položíme derivaci ![Math $[\xi \xi ]'\ =\ 0$](/wiki/lib/exe/fetch.php?media=wiki:latex:/img99956dab4830c669109918cdd304db9e.png) :
:
![Equation $$
{\left.\frac{\partial \left[\xi \xi \right]}{\partial \omega }\right|}_{\omega ={\omega }_0}=-\left[x{{\rm '}}x{{\rm '}}\right]\cdot {\rm sin}\left(2{\omega }_0\right){\rm +2}\left[x{{\rm '}}y{{\rm '}}\right]\cdot {\rm cos}\left({\rm 2}{\omega }_0\right)+\left[{{\rm y}}{{\rm '}}{{\rm y}}{{\rm '}}\right]\cdot {\rm sin}\left({\rm 2}{\omega }_0\right)=0.
$$](/wiki/lib/exe/fetch.php?media=wiki:latex:/img5cc22d3a2dce0c71ca27bb373a57925c.png)
![Math $[\eta \eta ]'$](/wiki/lib/exe/fetch.php?media=wiki:latex:/imge205109c8f8e7e4a11ac04af8888ae60.png) , takže:
, takže:
![Equation $$
{\rm tg}\left({\rm 2}{\omega }_0\right){\rm =}\frac{{\rm 2}\left[x{{\rm '}}y{{\rm '}}\right]}{\left[x{{\rm '}}x{{\rm '}}\right]{\rm -}\left[{{\rm y}}{{\rm '}}{{\rm y}}{{\rm '}}\right]}.
$$](/wiki/lib/exe/fetch.php?media=wiki:latex:/imgbc625b91491aeebbe7b3ca74d3973da7.png)
 může ležet např. v 1. nebo 3. kvadrantu a dá dvě hodnoty:
může ležet např. v 1. nebo 3. kvadrantu a dá dvě hodnoty:  a
a  , což platí pro obě hlavní osy (
, což platí pro obě hlavní osy ( proti směru hodinových ručiček. V případě
proti směru hodinových ručiček. V případě ![Math $[x'y']\ \approx \ 0$](/wiki/lib/exe/fetch.php?media=wiki:latex:/img79d5214ac7b03dd6aeb6adb0ef2b7a8c.png) bude i
bude i  .
.
 ) vypočítáme empirické střední souřadnicové chyby s kontrolou:
) vypočítáme empirické střední souřadnicové chyby s kontrolou:
![Equation $$
m^2_x=\frac{\left[x{{\rm '}}x{{\rm '}}\right]}{n-1} , m^2_y=\frac{\left[y{{\rm '}}y{{\rm '}}\right]}{n-1} ,cov\left(x,y\right)=m_{xy}=\frac{\left[x{{\rm '}}y{{\rm '}}\right]}{n-1} , \frac{2m_{xy}}{m^2_x-m^2_y}={\rm tg}\left({\rm 2}{\omega }_0\right) .
$$](/wiki/lib/exe/fetch.php?media=wiki:latex:/imgeb20edc9549aa9ac557d3c114f804107.png)
 , protože se jedná o opravy vzhledem k aritmetickým průměrům
, protože se jedná o opravy vzhledem k aritmetickým průměrům ![Math $[x]:n$](/wiki/lib/exe/fetch.php?media=wiki:latex:/imga872d0e4a00aeb2706dc5d7ae349576a.png) ,
, ![Math $[y]:n$](/wiki/lib/exe/fetch.php?media=wiki:latex:/img5ed56565e9ac3eaa757b1678ea1eef82.png) . Střední chyby v extrémních směrech vypočítáme pro kontrolu dvojmo z rovnic:
. Střední chyby v extrémních směrech vypočítáme pro kontrolu dvojmo z rovnic:
![Equation $$
m^2_{\xi }=\frac{\left[\xi \xi \right]}{n-1}=m^2_x\cdot {{\cos }^2 \left({\omega }_0\right)\ }+m_{xy}\cdot {\sin \left(2{\omega }_0\right)\ }+m^2_y\cdot {{\sin }^2 \left({\omega }_0\right)\ },
$$](/wiki/lib/exe/fetch.php?media=wiki:latex:/imga59ee7f33037a59fd57b8ecfd9e4e04c.png)
![Equation $$
m^2_{\eta }=\frac{\left[\eta \eta \right]}{n-1}=m^2_x\cdot {{\sin }^2 \left({\omega }_0\right)\ }-m_{xy}\cdot {\sin \left(2{\omega }_0\right)\ }+m^2_y\cdot {{\cos }^2 \left({\omega }_0\right)\ }.
$$](/wiki/lib/exe/fetch.php?media=wiki:latex:/img64dac7fb268f72033ae5e83acc0b0950.png)
 bude
bude
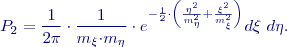
 ,
,  . Elipsa chyb má důležité místo při zjednodušeném posuzování přesnosti určované polohy bodu.
. Elipsa chyb má důležité místo při zjednodušeném posuzování přesnosti určované polohy bodu.
 jsou neznámé
jsou neznámé  (úhlů, směrů, délek), budou empirické střední chyby ve směru os
(úhlů, směrů, délek), budou empirické střední chyby ve směru os
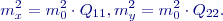

 ,
,  a
a  dostaneme
dostaneme
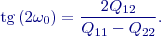
 ,
,  .
.
 ,
,  vynesené ve směru původních os
vynesené ve směru původních os