|
Obsah
« 18. Metody robustního odhadu 19. Metody řešení normálních rovnicb ÚvodMetodu volíme podle počtu rovnic a možnosti použití výpočetní techniky. K dispozici je velké množství metod, ať už vhodných pro případné ruční nebo počítačové zpracování. Zde budou zmíněny pouze některé vybrané metody, které se tradičně využívají a dále některé metody poskytující vyšší spolehlivost výsledků zejména z hlediska numerické přesnosti. Metody detailně popsané lze nalézt např. v [1] a [2], algoritmy jsou podrobně uvedeny (včetně zdrojových kódů) také v [3] (případně v [4]). Základní třídění prezentovaných metod řešení vyrovnávacích úloh:
Jednotlivé metody nyní budou postupně popsány tak, aby byl zřejmý jejich princip a možnosti. K využití pseudoinverze je vhodné poznamenat, že jednotlivá využití vyplývají z jejích vlastností a proto jí bude věnována samostatný odstavec, kde budou popsány vlastnosti, postupy výpočtu a posléze jednotlivé možnosti využití. Vzhledem k tomu, že v současné době je běžné řešení velkých a špatně podmíněných soustav, lze tuto kapitolu doporučit zejména vzhledem k možnostem, které poskytuje singulární rozklad. Při použití mnohých metod je z numerického hlediska pro zajištění proveditelnosti a kvality výpočtu vhodné provést přeskládání řešené matice nebo celé soustavy částečným nebo úplným výběrem hlavního prvku, s využitím permutační matice. Tomuto tématu bude věnován samostatný odstavec na konci kapitoly. Výpočet inverzní maticeVe všech předchozích odvozeních se řešení normálních rovnic provádí inverzí čtvercové matice. Numerické řešení inverze není triviální záležitostí, v mnoha případech je také numericky nestabilní a představuje největší problém při řešení vyrovnání. K dispozici je nepřeberné množství metod, např. v [5] lze nalézt metodu založenou na výpočtu determinantů, inverze matice rozdělením na bloky a další, které se pro inverzi matice o větším počtu řádků/sloupců nehodí. Dále proto budou uvedeny vybrané metody vhodné pro počítačové řešení o reálně využitelném počtu neznámých.
Pro inverzní matici
kde Jordanův algoritmus
Podle [6] se invertovaná čtvercová matice
Stejně jako u všech metod založených na Gaussově eliminaci je vhodné aplikovat výběr hlavního prvku před začátkem ekvivalentních úprav. LU rozkladZákladem algoritmů inverze matic je vždy nějaká forma rozkladu (faktorizace) invertované matice na součin jednoduše invertovatelných matic. V případě LU rozkladu se jedná o trojúhelníkový rozklad čtvercové invertované matice tak, aby např. podle [7] platilo:
kde
Inverzní matice se pak vypočítá podle vzorce
Výpočet inverze dolní trojúhelníkové matice je jednoduchý, vždy je to také dolní trojúhelníková matice, na diagonále jsou reciproké hodnoty odpovídajících si prvků původní matice a ostatní prvky lze postupně dopočítat. Zde uvedeme pouze pro dolní trojúhelníkovou matici:
V rovnici
LU rozklad je založen na stejném principu jako Gaussova eliminace, neřeší se však pouze soustava rovnic, ale rozkládá se matice na součin dvou snadno invertovatelných matic. QR rozklad
Rozklad matice na ortonormální matici
Každá čtvercová matice
Jestliže Pro výpočet inverzní matice pak platí:
Protože
kde
Výpočet ortonormální matice
pro
kde symbol
Rozklad lze provést také pro obdélníkovou matici
Jestliže
Numerickou stabilitu výpočtu lze zlepšit pomocí permutační matice
Z toho inverzní matice:
Přímé řešení normálních rovnicGaussova eliminační metodaPodstata Gaussovy eliminační metody je řečena již v názvu. Jednoduchými matematickými operacemi (násobení, sčítání) - redukcemi, dosáhneme postupné eliminace jednotlivých neznámých. Výpočet je mechanicky upraven do algoritmu. Postup redukcí bude ukázán na jednoduchém příkladu. Zvolme soustavu tří normálních rovnic:
První neznámou eliminujeme tak, že násobíme první rovnici postupně zlomky:
Je to tzv. první redukce normálních rovnic, kde dostaneme počet rovnic zmenšený o jednu:
Pro redukované členy zavedeme Gaussovo označení, např.
Podílem
kterou napíšeme s Gaussovými symboly:
Tato druhá redukce dává již jen jednu rovnici o jedné neznámé. Při čtyřech neznámých by přibyla čtvrtá normální rovnice a byly by nutné tři redukce. K výpočtu neznámých použijeme vždy první rovnice z původních a postupně redukovaných rovnic:
z nichž určíme postupně neznámé:
Postupným dosazením za
Algoritmus řešení lze tedy jednoduše vyjádřit pro soustavu normálních rovnic v maticovém vyjádření
Pro dosažení správného a přesného řešení je vhodné před řešením soustavy provést přeskládání (pivoting) soustavy. Choleskyho metoda
Je vhodná pro řešení tzv. špatně podmíněných soustav rovnic. Také je významně rychlejší, vyžaduje
Rozklad je unikátní, existuje pouze jedna dolní trojúhelníková matice s pozitivními hodnotami na diagonále, pokud jsou hodnoty matice
který se rozdělí na dvě na ekvivalentní rovnice:
Nejprve se určí neznámé
Označí-li se prvky matice
 : :
Dále výpočet ekvivalentních rovnic:
Pro
pro
Zápis rozkladu matice
Pro odstranění nutnosti výpočtu odmocniny lze použít podobný rozklad:
Pro rozklad pak platí:
Další výpočet probíhá obdobně, jako v předchozím případě, případně lze místo dvou soustav postupně řešit tři (více např. v [11]).
Matici Metoda postupné iterace
Tato metoda je vhodná pro řešení velikých systémů rovnic, kde přesné metody již nelze použít buď pro rozsah rovnic, nebo pro potřebnou přesnost. Princip metody je takový, že řešený systém
kde
Takový systém nelze řešit přímo, ale zpravidla lze použít iterace. Při prvém přiblížení dosadíme libovolný vektor
Po vzájemném postupném dosazení dostaneme:
Aby
To nenastává vždy. Podmínka nutná a postačující požaduje, aby všechna vlastní čísla matice Nedostatkem této metody je, že konverguje jen při splnění určitých podmínek a není proto použitelná pro všechny systémy. Výpočetní postup iterace může být dvojí:
U druhého způsobu je zpravidla rychlejší konvergence k limitám, avšak záleží také na pořadí počítaných neznámých. PseudoinverzePseudoinverzní matice a její výpočet má při řešení rozsáhlejších úloh v geodézii stále větší uplatnění, tento odstavec je věnován popisu vlastností a možnostem výpočtu. Vyplynou z toho praktické aplikace při řešení vyrovnání metodou nejmenších čtverců, které budou podrobněji popsány v následujících odstavcích. Pojem pseudoinverze je rozšířením inverze na matice, které invertovat nelze, tj. i na matice singulární a obdélníkové. Pseudoinverze jsou různé, tj. splňují různé podmínky, pro uváděné výpočty bude dále pojmem pseudoinverze označována pouze Moore-Penroseova pseudoinverze, která byla popsána a propracována v literatuře [12], [13] a [14]. Pro další studium i souvisejících problémů lze doporučit také [15]. Zde budou uvedeny jen některé postupy a algoritmy, které ilustrují výpočet a jeho vlastnosti. Definice a vlastnosti pseudoinverze
Pokud pseudoinverze
Tato pseudoinverzní matice existuje vždy a je jedinečná. Pokud nesplňuje některé uvedené vlastnosti, může se jednat o některý typ generalizované inverze, kterou však nelze obecně použít pro všechny dále popsané účely. Vybrané základní vlastnosti Moore-Penroseovi pseudoinverze:
Metody výpočtu pseudoinverzní maticeVýpočet pseudoinverzní matice lze provést mnoha různými metodami, zde bude uvedena metoda rozkladu na submatice, dále aplikačně velmi jednoduchá iterační metoda Ben Israela a Cohena a jako poslední nejvyužívanější metoda založená na singulárním rozkladu. Rozklad na součin matic
Pseudoinverzní matici k matici
lze vypočítat podle vztahu:
Obdélníkové matice Iterační metoda Ben-Israela a Cohena
Metoda je velmi jednoduchá, má zajištěnou konvergenci při dodržení triviálního pravidla. Nevýhodou je vyšší počet iterací. Jestliže
kde
kde
kde
kde
kde Pokud podmínka není splněna, posloupnost nemusí konvergovat. Metoda konverguje kvadraticky v „blízkosti“ výsledné pseudoinverzní matice, než se však dostane do této blízkosti, je to obvykle velmi výpočetně náročné. Metodu lze použít pro zpřesnění pseudoinverzní matice určené jinou metodou. Iterace se ukončí při dosažení požadované přesnosti, např. pokud je splněno kritérium:
kde Metoda využívající singulární rozkladZákladem tohoto výpočtu pseudoinverzní matice je výpočet vlastních vektorů a vlastních čísel matice (jak bude uvedeno dále), nejpoužívanějším postupem je vzhledem k jeho stabilitě je Golub-Reinschův postup, který je založen na transformaci do bidiagonálního tvaru pomocí Householderovy transformace, dále vytvoření tridiagonální symetrické matice a následně aplikováním QR rozkladu, blíže např. viz [17]. Zde bude uveden jednodušší a méně kvalitní postup.
Singulární rozklad je rozklad matice
Protože pseudoinverze ortogonální matice je rovná její transpozici, platí:
Pseudoinverzní matice diagonální matice se vypočítá také velmi jednoduše, výsledkem je diagonální matice, která se z nenulových prvků původní matice určí takto
Samotný výpočet pseudoinverzní matice je tedy triviální, nyní k principu výpočtu singulárního rozkladu. Zde se určují vlastní čísla matice
jejímž výsledkem je matice
Posloupnost
Matice
Matice
V případě, že vstupní matice pro výpočet pseudoinverze již je symetrická matice normálních rovnic, lze s výhodou vynechat první krok řešení, tj. tvorbu symetrické matice Využití pseudoinverze při řešení vyrovnání MNČVyužití pseudoinverze při řešení úloh metodou nejmenších čtverců je několikeré, některé možnosti budou dále popsány. Výpočet inverzní matice pseudoinverzí
Jak již bylo uvedeno, pokud existuje k dané matici matice inverzní, je totožná s maticí pseudoinverzní a lze tedy využít algoritmy pro výpočet pseudoinverzní matice, která na rozdíl od inverzní matice existuje vždy a výpočetní algoritmy zvládnou vyřešit i špatně podmíněné matice, u kterých výpočet inverze selhává. Zároveň lze s výhodou využít vlastností singulárního rozkladu, kdy se vlastní čísla matice v matici
kde Přímé řešení rovnic oprav pseudoinverzí
Jednou z vlastností Moore-Penroseovy pseudoinverze velmi dobře využitelnou pro řešení vyrovnání metodou nejmenších čtverců je minimalizace normy přeurčených systémů lineárních rovnic ve tvaru
kde
tj. splňuje podmínku metody nejmenších čtverců
Při využití vah pro nezávislá měření při vyrovnání se provede rozklad matice normálních rovnic ve smyslu
a řeší se rovnice ve tvaru
Řešení inverze singulární matice normálních rovnic
V případě, že matice
Řešení se provádí pomocí pseudoinverzní matice
Pro výpočet matice
Je to vzorec odlišný, než bychom čekali z analogie s regulární maticí. Pouze při
[1],
[15],
[17]
Björck, A.: Numerical Methods for Least Squares Problems. Society for Industrial and Applien Mathematics, Philadelphia, 1996. ISBN 0-89871-360-9.
[2],
[10],
[11]
Golub, G. H. - Van Loan, Ch. F.: Matrix computations. John Hopkins University Press, London, 1996. (3rd ed.) ISBN 0-8018-5414-8.
[3]
Press, W. H. - Flannery, B. P. - Teukolsky, S. A. - Vetterling, W. T.: Numerical Recipes. The Art of Scientific Computing. Cambridge University Press, 2007. ISBN 0-5218-8068-8.
[4],
[18]
Press, W. H. - Flannery, B. P. - Teukolsky, S. A. - Vetterling, W. T.: Numerical Recipes in Pascal. Cambridge University Press, 1989. ISBN 0-5213-7516-9.
[5],
[6],
[7],
[9]
Bubeník, F. - Pultar, M.: Matematické vzorce a metody. Vydavatelství ČVUT, Praha, 1994.
[8]
http://en.wikipedia.org/wiki/QR_decomposition; 6.1.2011.
[12]
Moore, E. H.: On the reciprocal of the general algebraic matrix. Bulletin of the American Mathematical Society 26: 394-395, 1920.
[13]
Bjerhammar, A.: Application of calculus of matrices to method of least squares; with special references to geodetic calculations. Trans. Roy. Inst. Tech. Stockholm 49, 1951.
[14]
Penrose, R.: A generalized inverse for matrices. In: Proceedings of the Cambridge Philosophical Society 51: 406-413, 1955.
[16]
Ben Israel, A. - Cohen, D.: On Iterative Computation of Generalized Inverses and Associated Projections. SIAM Numer. Anal., vol. 3, no. 3, USA, 1966.
« 18. Metody robustního odhadu |
 k čtvercové matici
k čtvercové matici  platí:
platí:

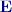 je jednotková matice (tj. matice s jedničkami na diagonále a nulami všude jinde). Inverzní matice existuje vždy, pokud je matice
je jednotková matice (tj. matice s jedničkami na diagonále a nulami všude jinde). Inverzní matice existuje vždy, pokud je matice 

 je dolní trojúhelníková matice a
je dolní trojúhelníková matice a  horní trojúhelníková matice. Rozklad existuje, pokud je matice
horní trojúhelníková matice. Rozklad existuje, pokud je matice 

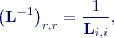

 značí pořadí řádku,
značí pořadí řádku,  pořadí sloupce. Odvození vychází ze vztahů jednoduše ilustrovaných v následujících rovnicích:
pořadí sloupce. Odvození vychází ze vztahů jednoduše ilustrovaných v následujících rovnicích:
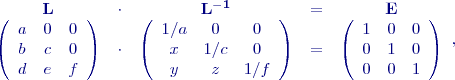
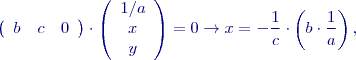
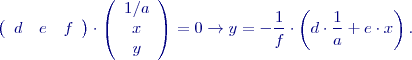
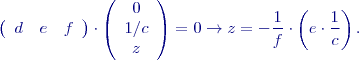
 a horní trojúhelníkovou matici
a horní trojúhelníkovou matici  , využívá se často právě při řešení úloh metodou nejmenších čtverců a také při výpočtu vlastních čísel.
, využívá se často právě při řešení úloh metodou nejmenších čtverců a také při výpočtu vlastních čísel.



 skládá z
skládá z  vektorů
vektorů
![Math ${\mathbf D}=[ \begin{array}{ccc}
{{\mathbf d}}_1 & \dots & {{\mathbf d}}_n \end{array}
]$](/wiki/lib/exe/fetch.php?media=wiki:latex:/img2e40575b74de585d929f1f1b209685d3.png) , ortonormální matice
, ortonormální matice ![Math ${\mathbf O}{\mathbf = }\left[ \begin{array}{ccc}
{{\mathbf o}}_1 & \dots & {{\mathbf o}}_n \end{array}
\right]$](/wiki/lib/exe/fetch.php?media=wiki:latex:/img0a90b0719117c4ac4409e1129a090eb1.png) , která se skládá z
, která se skládá z 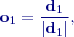
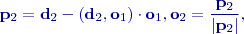
 :
:
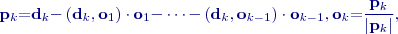
 značí skalární součin a
značí skalární součin a  velikost vektoru.
velikost vektoru.
 , kde
, kde  , ve tvaru:
, ve tvaru:

![Equation $${\mathbf A}{\mathbf =}{\mathbf Q}\cdot \left[ \begin{array}{c}
{{\mathbf R}}_1 \\
{\mathbf 0} \end{array}
\right]{\mathbf =}\left[ \begin{array}{cc}
{{\mathbf Q}}_{1_{(m\times n)}} & {{{\mathbf Q}}_2}_{(m\times (m-n))} \end{array}
\right]\cdot \left[ \begin{array}{c}
{{{\mathbf R}}_1}_{(n\times n)} \\
{\mathbf 0} \end{array}
\right]{\mathbf =}{{\mathbf Q}}_{1_{(m\times n)}}\cdot {{{\mathbf R}}_1}_{(n\times n)} .$$](/wiki/lib/exe/fetch.php?media=wiki:latex:/imgbffd20bd61af999a7106fca5dd6c795a.png)
 má maximální možný počet lineárně nezávislých řádků a diagonální prvky
má maximální možný počet lineárně nezávislých řádků a diagonální prvky  a
a  jsou unikátní,
jsou unikátní,  nikoli.
nikoli. je rovno hornímu trojúhelníkovému tvaru Choleskyho dekompozice matice
je rovno hornímu trojúhelníkovému tvaru Choleskyho dekompozice matice  .
.
 , kdy se přeskládají sloupce tak, aby diagonální prvky tvořily neklesající řadu. Rozklad pak má tvar:
, kdy se přeskládají sloupce tak, aby diagonální prvky tvořily neklesající řadu. Rozklad pak má tvar:


![Equation $$ \begin{array}{c}
\left[{pa}_{{\rm 1}}a_{{\rm 1}}\right]{dx}_{{\rm 1}}{\rm +}\left[pa_{{\rm 1}}a_{{\rm 2}}\right]dx_{{\rm 2}}{\rm +}\left[pa_{{\rm 1}}a_{{\rm 3}}\right]dx_{{\rm 3}}{\rm +[}pa_{{\rm 1}}l{\rm ']=0,} \\
\left[{pa}_{{\rm 1}}a_{{\rm 2}}\right]{dx}_{{\rm 1}}{\rm +}\left[{pa}_{{\rm 2}}a_{{\rm 2}}\right]{dx}_{{\rm 2}}{\rm +}\left[{pa}_{{\rm 2}}a_{{\rm 3}}\right]{dx}_{{\rm 3}}{\rm +[}{pa}_{{\rm 2}}l{\rm ']=0,} \\
\left[{pa}_{{\rm 1}}a_{{\rm 3}}\right]{dx}_{{\rm 1}}{\rm +}\left[{pa}_{{\rm 2}}a_{{\rm 3}}\right]{dx}_{{\rm 2}}{\rm +}\left[{pa}_{{\rm 3}}a_{{\rm 3}}\right]{dx}_{{\rm 3}}{\rm +[}{pa}_{{\rm 3}}l{\rm ']=0.} \end{array}
$$](/wiki/lib/exe/fetch.php?media=wiki:latex:/img5a1bc573261d9891ad0180cb693c6587.png)
![Math $-[pa_1a_2]/[pa_1a_1]$](/wiki/lib/exe/fetch.php?media=wiki:latex:/imgbd0f0d200fb9cd4e7de68b5958905acf.png) a přičteme ji k rovnici druhé,
a přičteme ji k rovnici druhé,![Math $-[pa_1a_3]/[pa_1a_1]$](/wiki/lib/exe/fetch.php?media=wiki:latex:/img5287250cef2df45aea4cfc901dbf560e.png) a přičteme ji k rovnici třetí.
a přičteme ji k rovnici třetí.![Equation $$\left(\left[pa_2a_2\right]-\left(\frac{\left[pa_1a_2\right]}{\left[pa_1a_1\right]}\right)\cdot \left[pa_1a_2\right]\right)\cdot dx_2+\left(\left[pa_2a_3\right]-\left(\frac{\left[pa_1a_2\right]}{\left[pa_1a_1\right]}\right)\cdot \left[pa_1a_3\right]\right)\cdot dx_3+([pa_2l']-\{[pa_1a_2]/[pa_1a_1])\cdot [pa_1l'])=0, $$](/wiki/lib/exe/fetch.php?media=wiki:latex:/img32d3cc15b1b8bdf6b1ed387a4ebab146.png)
![Equation $$\left(\left[pa_2a_3\right]-\left(\frac{\left[pa_1a_3\right]}{\left[pa_1a_1\right]}\right)\cdot \left[pa_1a_2\right]\right)\cdot dx_2+\left(\left[pa_3a_3\right]-\left(\frac{\left[pa_1a_3\right]}{\left[pa_1a_1\right]}\right)\cdot \left[pa_1a_3\right]\right)dx_3+([pa_3l']-\ -([pa_1a_3]/[pa_1a_1])\cdot [pa_1l'])=0.$$](/wiki/lib/exe/fetch.php?media=wiki:latex:/imgd4ad7ecbeb6b053d1a0409cc1b698e46.png)
![Math $[pa_2a_2.1]$](/wiki/lib/exe/fetch.php?media=wiki:latex:/img7349204cb20936b9f31f2a04290d2a8b.png) , což znamená „
, což znamená „![Math $[pa_2a_2]$](/wiki/lib/exe/fetch.php?media=wiki:latex:/imgffadd1f7de5c2d64a98a3903700eca40.png) po první redukci“. Dostaneme tak dvě jednou redukované normální rovnice o dvou neznámých:
po první redukci“. Dostaneme tak dvě jednou redukované normální rovnice o dvou neznámých:
![Equation $$ \begin{array}{c}
\left[{pa}_2a_2.1\right]\cdot {dx}_2+\left[{pa}_2a_3.1\right]\cdot {dx}_3+[{pa}_2l'.1]=0,\ \\
\left[{pa}_2a_3.1\right]\cdot {dx}_2+\left[{pa}_3a_3.1\right]\cdot {dx}_3+[{pa}_3l'.1]=0.\ \end{array}
$$](/wiki/lib/exe/fetch.php?media=wiki:latex:/imgc95a8c2da2104d8a95b2224a3ac1a729.png)
![Math $-[pa_2a_3.1]/[pa_2a_2.1]$](/wiki/lib/exe/fetch.php?media=wiki:latex:/imgecf27c671052ce9b917c5ec474b5d3bb.png) násobíme nyní první redukovanou rovnici, přičteme k druhé a dostaneme dvakrát redukovanou normální rovnici:
násobíme nyní první redukovanou rovnici, přičteme k druhé a dostaneme dvakrát redukovanou normální rovnici:
![Equation $$\left(\left[pa_3a_{3.1}\right]-\left(\frac{\left[pa_2a_{3.1}\right]}{\left[pa_2a_{2.1}\right]}\right)\cdot \left[pa_2a_{3.1}\right]\right)\cdot dx_3+\left(\left[pa_3l'.1\right]-\left(\frac{\left[pa_2a_{3.1}\right]}{\left[pa_2a_{2.1}\right]}\right)\cdot \left[pa_2l'.1\right]\right)=0$$](/wiki/lib/exe/fetch.php?media=wiki:latex:/img176124be0fbedb701fd4b078a118acf7.png)
![Equation $$\left[pa_3a_3.2\right]\cdot dx_3+[pa_3l'.2]=0. $$](/wiki/lib/exe/fetch.php?media=wiki:latex:/imge35dd7bcc6887f4b42c84a7105087173.png)
![Math $\left[{pa}_1a_1\right]\cdot {dx}_1+\ \left[{pa}_1a_2\right]\cdot {dx}_2+\left[{pa}_1a_3\right]\cdot {dx}_3+[{pa}_1l']=0 ,$](/wiki/lib/exe/fetch.php?media=wiki:latex:/imgac84fc913d97dcf3701a85fd8a5b850d.png)
![Math $\left[pa_2a_2.1\right]\cdot dx_2+\left[pa_2a_3.1\right]\cdot dx_3+[pa_2l'.1]=0$](/wiki/lib/exe/fetch.php?media=wiki:latex:/imgdcc0c721768b954558244e83d67f0c71.png) (po první redukci),
(po první redukci),
![Math $\left[pa_3a_3.2\right]\cdot dx_3+[pa_3l'.2]=0$](/wiki/lib/exe/fetch.php?media=wiki:latex:/img096dc6881a93832aca02d8b0d77217ea.png) (po druhé redukci),
(po druhé redukci),
![Equation $$dx_3=-[pa_3l'.2]/[pa_3a_3.2], $$](/wiki/lib/exe/fetch.php?media=wiki:latex:/imgcb1076a2781856e40ab2c8bf6afe08c9.png)
![Equation $$dx_2=-([pa_2l'.1]+\left[pa_2a_3.1\right]\cdot dx_3)/[pa_2a_2.1], $$](/wiki/lib/exe/fetch.php?media=wiki:latex:/img66bb58c7390a88befc3e38124a1b58e3.png)
![Equation $$dx_1=-([pa_1l']+\left[pa_1a_3\right]\cdot dx_3+\ \left[pa_1a_2\right]\cdot dx_2)/[pa_1a_1].$$](/wiki/lib/exe/fetch.php?media=wiki:latex:/imgf681bf0254e0a8b08d5716280d40d4e0.png)
 ,
,  na pravé straně bychom mohli případně každou neznámou vyjádřit obecně redukovanými měřeními
na pravé straně bychom mohli případně každou neznámou vyjádřit obecně redukovanými měřeními  .
.
 následujícím způsobem. Prvky matice
následujícím způsobem. Prvky matice  zahrneme jakoby do posledního sloupce matice
zahrneme jakoby do posledního sloupce matice  :
:




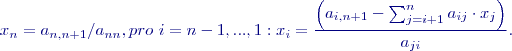
 operací oproti Gaussově eliminaci a pro získání stabilního a přesného řešení není třeba přeskládání prvků před řešením (pivoting). Řešení odpovídá rozkladu symetrické pozitivně definitní matice
operací oproti Gaussově eliminaci a pro získání stabilního a přesného řešení není třeba přeskládání prvků před řešením (pivoting). Řešení odpovídá rozkladu symetrické pozitivně definitní matice  :
:



 , poté
, poté  . Získat trojúhelníkovou matici lze např. algoritmem založeným na Gaussově eliminaci (
. Získat trojúhelníkovou matici lze např. algoritmem založeným na Gaussově eliminaci ( :
:

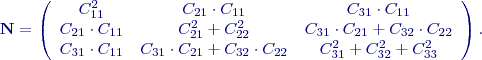
 , pak obecný algoritmus výpočtu pro matici
, pak obecný algoritmus výpočtu pro matici  vypadá takto:
vypadá takto:
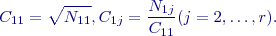
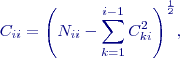
 , pro
, pro  .
.
 :
:
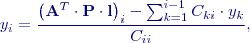
 :
:

![Equation $${\mathbf C}=\left( \begin{array}{cccc}
\sqrt{\left[pa_1a_1\right]} & \frac{\left[pa_1a_2\right]}{\sqrt{\left[pa_1a_1\right]}} & \frac{\left[pa_1a_3\right]}{\sqrt{\left[pa_1a_1\right]}} & \dots \\
0 & \sqrt{\left[pa_2a_2.1\right]} & \frac{\left[pa_2a_3.1\right]}{\sqrt{\left[pa_2a_2.1\right]}} & \dots \\
0 & 0 & \sqrt{\left[pa_3a_3.2\right]} & \dots \\
\vdots & \vdots & \vdots & \ddots \end{array}
\right). $$](/wiki/lib/exe/fetch.php?media=wiki:latex:/imgba36d743a157c4da72b6d2df99333601.png)
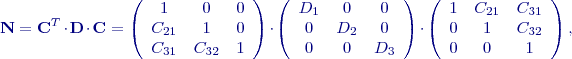
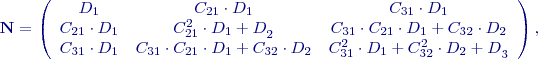
 , pro
, pro  ,
,
 , pro
, pro  .
.
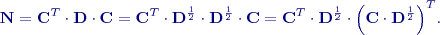
 převedeme na ekvivalentní:
převedeme na ekvivalentní:

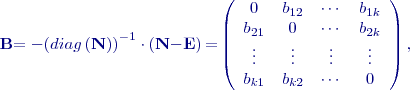

 do pravé strany rovnice a obdržíme „zlepšené“ hodnoty
do pravé strany rovnice a obdržíme „zlepšené“ hodnoty  . Při druhém přiblížení dosadíme
. Při druhém přiblížení dosadíme  atd. Tím obdržíme posloupnost vektorů:
atd. Tím obdržíme posloupnost vektorů:





 konvergovalo ke správné hodnotě, je nutné, aby konvergovala posloupnost:
konvergovalo ke správné hodnotě, je nutné, aby konvergovala posloupnost:

 byla menší než 1. Vlastní čísla ale většinou nebudeme počítat. Podmínkami postačujícími pro konvergenci dané posloupnosti je, aby kterákoliv norma matice
byla menší než 1. Vlastní čísla ale většinou nebudeme počítat. Podmínkami postačujícími pro konvergenci dané posloupnosti je, aby kterákoliv norma matice  matice
matice 

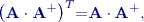
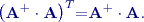
 .
. .
. .
. platí:
platí:  .
. .
. ,
, 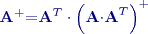 .
.

 tak, aby platilo
tak, aby platilo  (
( je hodnost příslušných matic).
je hodnost příslušných matic).
 :
:


 je limitou posloupnosti
je limitou posloupnosti  , jestliže reálné
, jestliže reálné 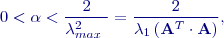
 je kvadrát maximálního vlastního čísla matice
je kvadrát maximálního vlastního čísla matice 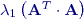 je maximální vlastní číslo symetrické matice
je maximální vlastní číslo symetrické matice  . Tato podmínka je obtížněji vyčíslitelná nežli následující „nižší“ horní hranice intervalu:
. Tato podmínka je obtížněji vyčíslitelná nežli následující „nižší“ horní hranice intervalu:
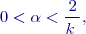
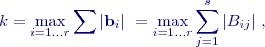

 je počet řádků a sloupců matice
je počet řádků a sloupců matice  ).
).

 je zvolené (malé kladné) číslo.
je zvolené (malé kladné) číslo.  , kde
, kde  je malé kladné číslo. Větší hodnota
je malé kladné číslo. Větší hodnota 
 jsou ortonormální matice (matice levých, resp. pravých vlastních vektorů matice
jsou ortonormální matice (matice levých, resp. pravých vlastních vektorů matice  je diagonální matice tvořená vlastními čísly matice
je diagonální matice tvořená vlastními čísly matice 

 . Nulové prvky zůstanou nulové.
. Nulové prvky zůstanou nulové.
 . Výpočtem QR rozkladu
. Výpočtem QR rozkladu  se získají matice
se získají matice 
 , která je podobná
, která je podobná 

 konverguje k trojúhelníkové matici s vlastními čísly na diagonále, jsou to vlastní čísla symetrické matice
konverguje k trojúhelníkové matici s vlastními čísly na diagonále, jsou to vlastní čísla symetrické matice 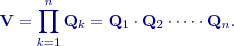

 stanovit následujícím způsobem:
stanovit následujícím způsobem:

 ,
,  a
a  značí maximální vlastní číslo matice.
značí maximální vlastní číslo matice.
 ve smyslu euklidovské normy tak, že pro všechna řešení
ve smyslu euklidovské normy tak, že pro všechna řešení 



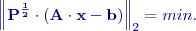
 . Řešení systému normálních rovnic splní podmínku
. Řešení systému normálních rovnic splní podmínku  a zapíšeme jej ve tvaru:
a zapíšeme jej ve tvaru:

 použijeme zákon hromadění vah s tím, že
použijeme zákon hromadění vah s tím, že 

 . V opačném případě je
. V opačném případě je  , kde
, kde  je symbol pro stopu matice
je symbol pro stopu matice