|
Obsah
« 19. Metody řešení normálních rovnic 20. Kritéria pro testování opakovaných měření ÚvodV geodetické praxi se velmi často opakuje měření určité veličiny a je vhodné kontrolovat, zda výsledky odpovídají předpokládané (očekávané) přesnosti. Mezní rozdílZa znalosti základní směrodatné odchylky měření je možno stanovit mezní odchylku rozdílu mezi dvěma měřeními. Směrodatná odchylka rozdílu dvou měření:
Mezní odchylka rozdílu dvou měření (mezní rozdíl):
Rozdíl by v ideálním případě byl roven nule. Pokud rozdíl překročí mezní hodnotu, měření nevyhovují přesnosti a je nutno přidat další měření. Pak se přesnost kontroluje podle McKay - Nairova testu (viz dále).
Hodnoty Testování oprav opakovaných měření od průměruV případě, že je měření více než dvě, lze je statisticky kontrolovat výpočtem průměru a následně oprav jednotlivých měření, jejichž velikost se pak testuje. Jednoduchý test opravSe zřetelem k normálnímu rozdělení oprav lze jako velmi orientační test připustit přibližné oboustranné testování oprav tak, že
 se volí 2 - 3. se volí 2 - 3.
McKay - Nairův test oprav při známé základní střední chybě
Vhodnější než předchozí možnost je test  pro McKay - Nairův test pro McKay - Nairův test
Pearson-Sekharův (Grubbsův) test oprav
Testuje se maximální oprava
kde
Tab. 2 Kritické hodnoty
Testování mezní opravy pomocí střední opravy
V daném výběrovém souboru o velikosti
která má speciální rozdělení analogické předchozímu odstavci, kritické hodnoty se vypočítají podle vzorce
kde
Tab. 3 Kritické hodnoty
Příliš odlehlým měřením bude to měření, které má největší opravu Ověřování hypotézy o odlehlosti krajních měření ve výběru z normálního rozděleníVýběrovým hodnotám (měřením), které se svou velikostí nápadné odlišují od ostatních a budí podezření, že nepatří do výběru, říkáme odlehlá měření. Testujeme hypotézu, že všechna měření patří do výběru z normálního rozdělení. Testování variačního rozpětí
Lze posuzovat diferenci krajních hodnot
Kritické hodnoty jsou v Tab. 4.
Tab. 4 Kritické hodnoty
Testování krajních hodnot náhodného výběru
Výběrové hodnoty seřadíme podle velikosti
které má speciální rozdělení pravděpodobnosti, které zde nebudeme uvádět a uvedeme pouze výtah z tabulek kritických hodnot
Příliš odlehlým bude to měření
[1]
Grubbs, F. E.: Sample criteria for testing outlaying observations. Annals of mathematical statistics, 21 (1950).
[2]
Grubbs, F. E.: Procedures for Detecting Outlying Observations in Samples. Technometrics, Vol. 11, No. 1 (Feb., 1969), pp. 1-21.
[3]
Janko, J.: Statistické tabulky. Nakladatelství československé akademie věd, Praha 1958.
« 19. Metody řešení normálních rovnic |
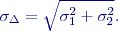
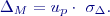
 tohoto oboustranného testu jsou
tohoto oboustranného testu jsou  pro
pro  a
a  pro
pro  , podle tabulek normálního rozdělení. Oboustranný test je to proto, že může rozdíl nabývat jak kladné, tak záporné hodnoty.
, podle tabulek normálního rozdělení. Oboustranný test je to proto, že může rozdíl nabývat jak kladné, tak záporné hodnoty.

 . Pokud oprava překročí maximální hodnotu, je vhodné nejméně jedno měření přidat. Pokud po dalším hodnocení není podmínka splněna, jedno měření se vyloučí, pokud maximální oprava opět nevyhoví, opět se jedno měření přidá atd. Kritické hodnoty jsou v
. Pokud oprava překročí maximální hodnotu, je vhodné nejméně jedno měření přidat. Pokud po dalším hodnocení není podmínka splněna, jedno měření se vyloučí, pokud maximální oprava opět nevyhoví, opět se jedno měření přidá atd. Kritické hodnoty jsou v 
 . Mechanismus testování je stejný jako v předchozím případě, pouze se vždy vypočítá výběrová střední chyba
. Mechanismus testování je stejný jako v předchozím případě, pouze se vždy vypočítá výběrová střední chyba  . Kritické hodnoty jsou v Tab. 2, mají speciální rozdělení pravděpodobnosti podle
. Kritické hodnoty jsou v Tab. 2, mají speciální rozdělení pravděpodobnosti podle 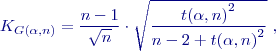
 je kritická hodnota hodnota Studentova rozdělení
je kritická hodnota hodnota Studentova rozdělení  pro
pro  stupně volnosti a hladinu významnosti pro oboustranný test
stupně volnosti a hladinu významnosti pro oboustranný test  a pro jednostranný test
a pro jednostranný test  .
.
 pro Pearson-Sekharův (Grubbsův) oboustranný test
pro Pearson-Sekharův (Grubbsův) oboustranný test
 vypočítáme výběrový průměr
vypočítáme výběrový průměr  a střední opravu
a střední opravu ![Math $m_v=\sqrt{\frac{\left[vv\right]}{n}}$](/wiki/lib/exe/fetch.php?media=wiki:latex:/img976e5d88fb69c9dca37ee6a189359fa8.png) , kde
, kde  ,
,  jsou měřené hodnoty. Vyhledáme opravu s maximální absolutní velikostí a mezní oprava se určí:
jsou měřené hodnoty. Vyhledáme opravu s maximální absolutní velikostí a mezní oprava se určí:


 pro vybraná
pro vybraná  je uvedena dále.
je uvedena dále.

 a pro které bude platit
a pro které bude platit  ; toto měření vyloučíme ze souboru a vypočítáme nový průměr, střední opravu a postup budeme případně opakovat pro další odlehlejší měření.
; toto měření vyloučíme ze souboru a vypočítáme nový průměr, střední opravu a postup budeme případně opakovat pro další odlehlejší měření.
 a
a  v daném výběru. Testovací kritérium:
v daném výběru. Testovací kritérium:

 pro testování variačního rozpětí
pro testování variačního rozpětí
 , vypočítáme z maximální hodnoty rozdílu dvou sousedních hodnot na krajích seřazeného výběru testovací kritérium
, vypočítáme z maximální hodnoty rozdílu dvou sousedních hodnot na krajích seřazeného výběru testovací kritérium
 nebo
nebo 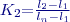
 pro různá
pro různá 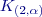
 (
( ), pro které bude platit
), pro které bude platit  , toto měření vyloučíme a postup budeme opakovat s případným dalším „podezřelým“ měřením.
, toto měření vyloučíme a postup budeme opakovat s případným dalším „podezřelým“ měřením.