|
Obsah
« 5. Vytyčení polohy bodu polární metodou 6. Vytyčení úsečky polární metodou ÚvodVytyčení úsečky je úloha, která se skládá z vytyčení dvou koncových bodů. Obvykle bývá z hlediska přesnosti vytyčení zadána přesností v poloze analogicky vytyčení polohy jednoho bodu, dále pak přesností rozměru (např. mezní odchylkou délky úsečky), přičemž tento parametr přesnosti bývá přísnější. Rozbory přesnosti před měřením se pak skládají ze dvou samostatných částí, kdy se zpracují požadavky na přesnost v poloze, dále je však také třeba provést rozbor pro požadavek na přesnost rozměru. Pro vytyčení se zvolí přísnější požadavek. Pro každý bod se vykonávají rozbory stejné jako při vytyčení bodu včetně závěrečné kontroly rozborem po měření, dále budou popsány pouze ty, které se týkají rozměru úsečky při vytyčení polární metodou z jednoho stanoviska. Rozbor přesnosti před měřením pro rozměr úsečkyPři vytyčení úsečky polární metodou jsou souřadnice koncových bodů dány:
kde Délka úsečky:
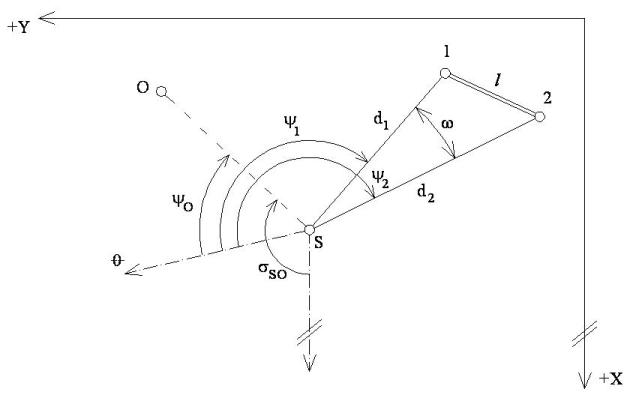
Obr. 1 Schema vytyčení úsečky Po dosazení, roznásobení a úpravě:
Pro libovolné úhly
Po úpravě tedy:
kde
Pak platí:
Toto odvození ukazuje, že délka vytyčené úsečky ve tvaru kosinové věty není závislá na stanovisku a jeho přesnosti, ani na orientaci a její přesnosti, ale pouze na vytyčeném úhlu (rozdílu vytyčených úhlů) a jeho přesnosti a na vytyčených délkách. Vliv centrace přístroje na stanovisku a cíle na orientaci se zde neuplatní, neboť délka je vytyčována z přístroje a tím centrací není narušen ani tvar, ani rozměr vytyčovaného obrazce. Vliv na přesnost vytyčované délky Nepřesnost (chyba souřadnic a centrace) na stanovisku a na orientaci působí stejně na oba vytyčované body a tedy výsledkem těchto chyb je pootočení a posun celého obrazce, nikoli jeho deformace či změna rozměru.
Přesnost vytyčení délky
Po aplikaci zákona hromadění směrodatných odchylek:
kde
Po dosazení:
Pro obvyklý případ, kdy se vytyčují obě délky se stejnou přesností
Po roznásobení a triviálních úpravách:
Rovnici lze symbolicky vyjádřit ve tvaru:
kde
Opět jsou zde dvě neznámé
Při volbě stanoviska vytyčení lze využít výhodné konfigurace, kdy se velmi málo projeví nepřesnost měření délek a chyba délky vytyčené úsečky je produktem zejména nepřesnosti vytyčení úhlu. Výhodnost jednotlivých konfigurací bude demonstrována v následující tabulce. Je zde vypočtena přesnost pro vytyčení úsečky
Obr. 2 Situace modelu přesnosti vytyčení úsečky (vlevo význam úhlu Tab. 1 Vliv jednotlivých složek a celková přesnost vytyčení délky úsečky
Obr. 3 Vliv jednotlivých složek a celková přesnost vytyčení délky úsečky - grafické znázornění
V uvedeném případě je příčná chyba způsobená nepřesností vytyčení úhlu významně menší než chyba vytyčení délky a tedy lze ve vhodné konfiguraci dosáhnout vyšší přesnosti než je přesnost přímého vytyčení délky. V uvedeném případě byla navíc zvolena směrodatná odchylka realizace
Pro úhel sevřený vytyčovanou úsečkou a spojnicí přístroj - střed úsečky Rozbor přesnosti při měření pro rozměr úsečkyKontrolují se přímo měřené veličiny v rámci kontroly vytyčení bodu, zvlášť není další kontrola pro rozměr úsečky možná. Rozbor přesnosti po měření pro rozměr úsečkyKontroluje se vlastní rozměr úsečky nezávisle, při kontrole je nutné uvážit také přesnost kontrolní metody. Lze použít např. pro krátké vzdálenosti měření pásmem nebo kontrola měřením vodorovných směrů a délek z vhodné konfigurace. Kontrola se provede porovnáním rozdílu kontrolně určené a projektované délky s mezním rozdílem:
kde
« 5. Vytyčení polohy bodu polární metodou |

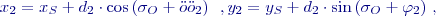
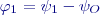 ,
,  , a
, a  ,
,  ,
,  jsou měřený a vytyčované směry na orientaci a body 1 a 2.
jsou měřený a vytyčované směry na orientaci a body 1 a 2.

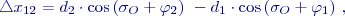
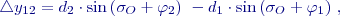

 a
a  platí:
platí:



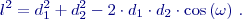
 má realizace, neboť zanáší chyby do vytyčených délek
má realizace, neboť zanáší chyby do vytyčených délek  ,
,  i úhlu
i úhlu  .
.
 ,
,  a
a  a konfigurací, tj. velikostí
a konfigurací, tj. velikostí  a
a  a přesnosti měření směrů
a přesnosti měření směrů  a
a  na body dána:
na body dána:
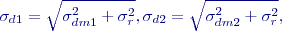
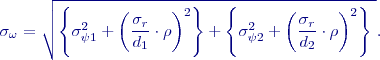
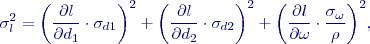



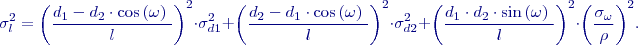
 lze vztah zjednodušit do tvaru:
lze vztah zjednodušit do tvaru:
![Equation $${\sigma }^2_l=\left[{\left(\frac{d_1-d_2\cdot {\cos \left(\omega \right)\ }}{l}\right)}^2+{\left(\frac{d_2-d_1\cdot {\cos \left(\omega \right)\ }}{l}\right)}^2\right]\cdot {\sigma }^2_d+{\left(\frac{d_1\cdot d_2\cdot {\sin \left(\omega \right)\ }}{l}\right)}^2\cdot {\left(\frac{{\sigma }_{\omega }}{\rho }\right)}^2 .$$](/wiki/lib/exe/fetch.php?media=wiki:latex:/imgdccb9e61b5cfaec60fc94c3868e2e3ff.png)
![Equation $${\sigma }^2_l=\left[2-\frac{d^2_1+d^2_2}{l^2}{\cdot \left({\sin \left(\omega \right)\ }\right)}^2\ \right]\cdot {\sigma }^2_d+{\left(\frac{d_1\cdot d_2\cdot {\sin \left(\omega \right)\ }}{l}\right)}^2\cdot {\left(\frac{{\sigma }_{\omega }}{\rho }\right)}^2 . $$](/wiki/lib/exe/fetch.php?media=wiki:latex:/imgbca41980f14fa880f096c7274512174d.png)
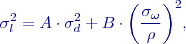
 a
a  jsou konstanty dané konfigurací. (Pro vyjímečný případ různých přesností vytyčovaných délek ve tvaru
jsou konstanty dané konfigurací. (Pro vyjímečný případ různých přesností vytyčovaných délek ve tvaru 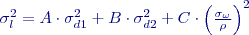 ).
).
 a
a  polární metodou z jednoho stanoviska v různých variantách natočení úsečky, které je charakterizováno úhlem
polární metodou z jednoho stanoviska v různých variantách natočení úsečky, které je charakterizováno úhlem  , směrodatná odchylka vytyčení délky je
, směrodatná odchylka vytyčení délky je  , směrodatná odchylka vytyčení úhlu je
, směrodatná odchylka vytyčení úhlu je  , směrodatná odchylka realizace je
, směrodatná odchylka realizace je 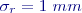 . Situace modelu je znázorněna na
. Situace modelu je znázorněna na 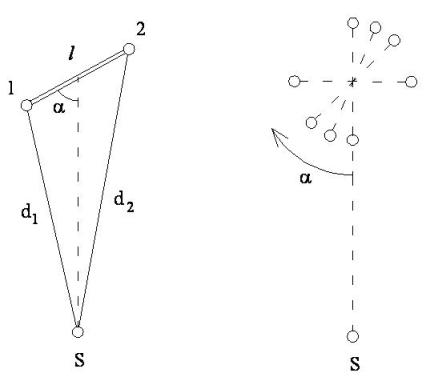





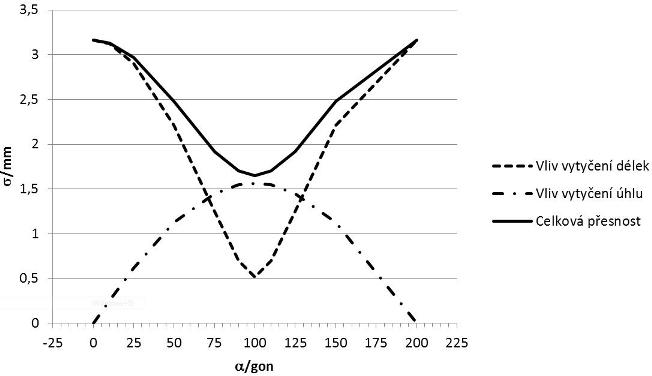
 je konfigurace nejpříznivější za předpokladu, že vliv vytyčení délek je větší než vliv vytyčení úhlu. V opačném případě je nejvhodnější konfiguraci případ
je konfigurace nejpříznivější za předpokladu, že vliv vytyčení délek je větší než vliv vytyčení úhlu. V opačném případě je nejvhodnější konfiguraci případ  .
.
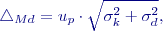
 je směrodatná odchylka kontrolní metody a
je směrodatná odchylka kontrolní metody a  je požadovaná směrodatná odchylka vytyčované úsečky.
je požadovaná směrodatná odchylka vytyčované úsečky.