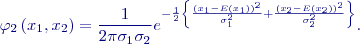|
Obsah
« 5. Intervalové odhady 6. Vícerozměrná náhodná veličina Úvod
Vícerozměrnou, přesněji
Její zákon rozdělení může být popsán ve formě tzv. sdružené distribuční funkce
Sdružená distribuční funkce má tyto vlastnosti:
Její hodnoty leží v intervalu
 nabude hodnoty z intervalu nabude hodnoty z intervalu 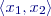 a současně náhodná veličina a současně náhodná veličina  hodnoty z intervalu hodnoty z intervalu  bude bude
tedy
Uvažujeme-li pouze pravděpodobnost, že náhodná veličina
a pravděpodobnost, že náhodná veličina
Vidíme, že se jedná o jednorozměrné distribuční funkce, které se nazývají marginální (okrajové) distribuční funkce veličiny
Jestliže každá veličina může nabýt pouze spočetného počtu hodnot (obě veličiny jsou diskrétní), vyjadřujeme jejich zákon rozdělení také sdruženými pravděpodobnostmi, že náhodná veličina
pro které platí:
A také platí:
Marginální pravděpodobnosti jsou součtem sdružených pravděpodobností přes všechny hodnoty druhé veličiny a označíme je podobně pomocí indexů 1,2:
U spojitých náhodných veličin
Indexem 2 u
Charakteristiky vícerozměrné náhodné veličiny
Základními charakteristikami dvojrozměrné náhodné veličiny
Všechny uvedené charakteristiky popisují rozdělení náhodných veličin, neříkají však nic o intenzitě (těsnosti) vztahu mezi oběma veličinami. Těsnost vztahu měří kovariancekovariance
Pro její výpočet se prakticky používá tvar
Na kovarianci je založen koeficient korelace
který je bezrozměrnou charakteristikou těsnosti lineárního vztahu mezi dvěma veličinami. Koeficient korelace nabývá hodnot z intervalu
Charakteristiky
Matice
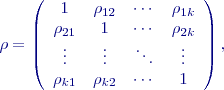
které lze sestavit do tzv. korelační matice
která je opět symetrická, protože platí Vícerozměrné normální rozdělení pravděpodobnosti
Z vícerozměrných normálních rozdělení je pro geodézii nejdůležitější dvojrozměrné normální rozdělení, což je rozdělení náhodné veličiny
kde
|
 -rozměrnou náhodnou veličinou budeme nazývat
-rozměrnou náhodnou veličinou budeme nazývat  .
.
 , která je definována jako pravděpodobnost, že náhodná veličina
, která je definována jako pravděpodobnost, že náhodná veličina  a současně náhodná veličina
a současně náhodná veličina  , tj.
, tj.

 , je funkcí neklesající a spojitou zleva vzhledem ke každé z náhodných veličin. Splňuje podmínky:
, je funkcí neklesající a spojitou zleva vzhledem ke každé z náhodných veličin. Splňuje podmínky:






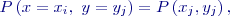
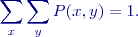
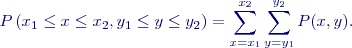
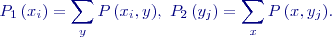
 existuje funkce
existuje funkce  taková, že
taková, že

 zdůrazňujeme, že se jedná o funkci dvojrozměrné náhodné veličiny. Funkce
zdůrazňujeme, že se jedná o funkci dvojrozměrné náhodné veličiny. Funkce  v bodě
v bodě  , splňující podmínku nerovnosti
, splňující podmínku nerovnosti  a podmínky
a podmínky
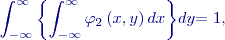
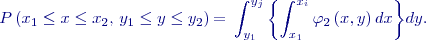
 , která je definována jako střední hodnota součinu odchylek obou veličin od jejich středních hodnot
, která je definována jako střední hodnota součinu odchylek obou veličin od jejich středních hodnot

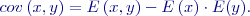
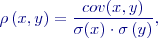
 . Jestliže je koeficient korelace nulový, potom veličiny
. Jestliže je koeficient korelace nulový, potom veličiny  se nazývají veličinami nekorelovanými. Tyto hodnoty nemusí být nezávislé, jelikož nulová hodnota korelačního koeficientu je nutnou, ale není podmínkou postačující pro nezávislost veličin. Může existovat velmi těsný, ale nelineární regresní vztah, na který není koeficient korelace citlivý.
se nazývají veličinami nekorelovanými. Tyto hodnoty nemusí být nezávislé, jelikož nulová hodnota korelačního koeficientu je nutnou, ale není podmínkou postačující pro nezávislost veličin. Může existovat velmi těsný, ale nelineární regresní vztah, na který není koeficient korelace citlivý.
 -rozměrné náhodné veličiny
-rozměrné náhodné veličiny 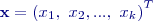 (náhodného vektoru) jsou střední hodnota
(náhodného vektoru) jsou střední hodnota 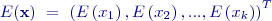 a kovariance společně s variancemi ve formě kovarianční matice
a kovariance společně s variancemi ve formě kovarianční matice  při označení
při označení  a
a  .
.
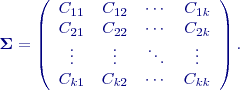
 , na hlavní úhlopříčce jsou variance jednotlivých veličin. Z prvků kovarianční matice mohou být vypočteny hodnoty korelačních koeficientů
, na hlavní úhlopříčce jsou variance jednotlivých veličin. Z prvků kovarianční matice mohou být vypočteny hodnoty korelačních koeficientů
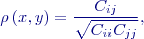
 .
.
 se sdruženou hustotou pravděpodobnosti
se sdruženou hustotou pravděpodobnosti

 ,
,  jsou střední hodnoty,
jsou střední hodnoty,  a
a  variance a
variance a  koeficient korelace mezi oběma veličinami. V případě nezávislosti obou veličin je
koeficient korelace mezi oběma veličinami. V případě nezávislosti obou veličin je  a jejich sdružená hustota pravděpodobnosti je
a jejich sdružená hustota pravděpodobnosti je