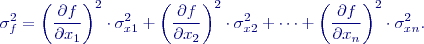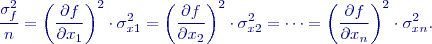|
Obsah
« 1. Rozbory přesnosti v inženýrské geodézii 2. Rozbory před měřením ÚvodRozbor před měřením slouží k výběru vhodné metody měření, případně také ke stanovení konkrétního počtu měření jednotlivé veličiny. Klade se důraz nejen na splnění požadované přesnosti, ale také na hospodárné měření. Nejprve se zvolí metoda měření na základě účelu, požadované přesnosti a dostupného vybavení, dále se zvolí a vypočítají požadované přesnosti přímo měřených veličin a posléze se určí nutné počty opakování měření jednotlivých veličin. Výpočet požadované směrodatné odchylky geodetických prací
Požadovaná přesnost může být zadána různými způsoby; pro potřeby rozboru přesnosti je nutné vždy vypočítat požadovanou směrodatnou odchylku
Z požadavku zanedbatelného vlivu na průběh stavebních prací (geodetické měření charakterizované kvadrátem mezní odchylky
kde Pokud je tento požadavek nesplnitelný anebo pouze s vynaložením neúměrných nákladů, lze v odůvodněných případech využít část větší, tato by neměla překročit hranici, kdy podíl geodetické a stavební části odchylky je stejný. Pak platí:
Z mezní odchylky se na směrodatnou přejde podle známého vztahu:
Jednorozměrný případ rozboru před měřením
Dále je třeba vybrat takovou metodu a postup, aby splnila požadovanou směrodatnou odchylku
Takto zapsáno se jeví rozbor přesnosti jako záležitost velmi jednoduchá, což platí v případě, že je přímo určována jednorozměrná veličina, např. má být určen úhel s mezní odchylkou
Mírně složitější je případ, kdy je znám funkční vztah mezi měřenou a určovanou veličinou jako je např. paralaktické měření délek. Je dána požadovaná mezní odchylka
(Nepřesnost délky základnové latě, resp. její oprava z komparace je pro potřeby rozboru přesnosti zanedbána, včetně nepřesnosti jejího určení). Závislost směrodatné odchylky délky
(platí za předpokladu, že
Protože se jedná o úlohu jednoduchou, lze zvolit Dvou a vícerozměrný případ rozboru před měřenímV případě dvou či vícerozměrného požadavku na přesnost výsledku geodetických prací jako je např. směrodatná odchylka polohová nebo souřadnicová neexistuje jednoznačné rozdělení požadavků do jednotlivých směrů a je nutné volit podle možností podmínku rozdělení. Může to být např. zásada stejného vlivu, kdy se výpočet provede za podmínky, že všechny jednotlivé členy charakterizující vliv měřených veličin jsou stejně velké. Pro funkci měřených veličin:
se směrodatná odchylka pomocí zákona hromadění směrodatných odchylek určí:
Volba přesnosti dle zásady stejného vlivu pak je:
Lze také volit přesnosti měření určitých veličin a dopočet dalších nebo výpočet prostým odhadem upřesňovaným iteračně. Možnosti jsou v tomto směru rozmanité, pro využití pro potřeby inženýrské geodézie budou prakticky ilustrovány na příkladech. Je třeba vždy zvážit, o kolika rozměrný problém se jedná a podle toho volit koeficient spolehlivosti, jsou zde značné rozdíly.
« 1. Rozbory přesnosti v inženýrské geodézii |
 měření, která je základem dalšího výpočtu. Běžně bývá požadovaná přesnost zadána prostřednictvím (stavební) tolerance
měření, která je základem dalšího výpočtu. Běžně bývá požadovaná přesnost zadána prostřednictvím (stavební) tolerance  nebo mezní odchylky
nebo mezní odchylky  . Tolerance definuje interval, ve kterém se musí nacházet výsledná výrobní realizace, a obsahuje tedy prostor pro chyby nejen ze strany geodetů, ale také jiných profesí. Musí se tedy využít pouze část toho intervalu, často to bývá 1/5 (podle ČSN 73 0420), tedy pro mezní odchylku geodetických prací platí:
. Tolerance definuje interval, ve kterém se musí nacházet výsledná výrobní realizace, a obsahuje tedy prostor pro chyby nejen ze strany geodetů, ale také jiných profesí. Musí se tedy využít pouze část toho intervalu, často to bývá 1/5 (podle ČSN 73 0420), tedy pro mezní odchylku geodetických prací platí:

 je o řád, tj. 10x přesnější nežli kvadrát stavební odchylky, lze odvodit pro mezní vytyčovací odchylku:
je o řád, tj. 10x přesnější nežli kvadrát stavební odchylky, lze odvodit pro mezní vytyčovací odchylku:



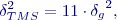

 je mezní symetrická odchylka,
je mezní symetrická odchylka,  je mezní odchylka rozměru stavebního dílce a
je mezní odchylka rozměru stavebního dílce a  je mezní odchylka montážní.
je mezní odchylka montážní.
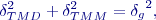



 je koeficient spolehlivosti, což odpovídá normované veličině normálního rozdělení
je koeficient spolehlivosti, což odpovídá normované veličině normálního rozdělení  . Koeficient spolehlivosti se pro potřeby geodetických rozborů přesnosti volí obvykle v rozmezí 2 až 3,5. Detailně je volba koeficientu spolehlivosti popsána v jiném článku. Je vhodné ještě poznamenat, že vzhledem k různým podmínkám a postupům využívaných při geodetickém měření se běžně volí různé hodnoty
. Koeficient spolehlivosti se pro potřeby geodetických rozborů přesnosti volí obvykle v rozmezí 2 až 3,5. Detailně je volba koeficientu spolehlivosti popsána v jiném článku. Je vhodné ještě poznamenat, že vzhledem k různým podmínkám a postupům využívaných při geodetickém měření se běžně volí různé hodnoty  , která vyhovuje buď přímo anebo při malém počtu opakování. Počet opakování se pak určí zaokrouhlením
, která vyhovuje buď přímo anebo při malém počtu opakování. Počet opakování se pak určí zaokrouhlením  vždy nahoru:
vždy nahoru:

 krát, neboť výsledkem je průměr ze dvou měření či vytyčení. Jen vyjímečně se měří či vytyčuje vícekrát nezávisle.
krát, neboť výsledkem je průměr ze dvou měření či vytyčení. Jen vyjímečně se měří či vytyčuje vícekrát nezávisle.
 . Je k dispozici přesný přístroj, který v jedné skupině měří úhel se směrodatnou odchylkou
. Je k dispozici přesný přístroj, který v jedné skupině měří úhel se směrodatnou odchylkou  . Požadovaná směrodatná odchylka je pak
. Požadovaná směrodatná odchylka je pak  a
a  , a tedy je zcela formálně úhel třeba měřit ve třech skupinách.
, a tedy je zcela formálně úhel třeba měřit ve třech skupinách.
 určení vodorovné délky
určení vodorovné délky  , je známo, že paralaktický úhel měřený v jedné poloviční laboratorní jednotce je určen s přesností
, je známo, že paralaktický úhel měřený v jedné poloviční laboratorní jednotce je určen s přesností  a pro výpočet délky z paralaktického úhlu na lať Zeiss Bala o délce
a pro výpočet délky z paralaktického úhlu na lať Zeiss Bala o délce  platí:
platí:
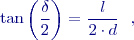

 na směrodatné odchylce paralaktického úhlu
na směrodatné odchylce paralaktického úhlu 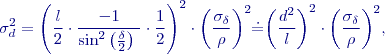
 je malé a tedy
je malé a tedy  ).
).
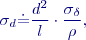
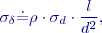
 a tedy požadovaná směrodatná odchylka měřené délky je
a tedy požadovaná směrodatná odchylka měřené délky je  , z toho podle předchozího vzorce vyplývá požadovaná směrodatná odchylka určeného paralaktického úhlu
, z toho podle předchozího vzorce vyplývá požadovaná směrodatná odchylka určeného paralaktického úhlu  a počet opakování měření
a počet opakování měření  .
.