|
« 10. Zákon hromadění středních chyb 11. Zákon hromadění chyb při působení systematických chyb ÚvodObecný zákon hromadění chyb platí i pro závislé veličiny, jejichž závislost je způsobena vlivem systematických chyb. V četných případech praxe jej můžeme zjednodušit. V maticovém zápise není také vidět působení vlivů jednotlivých druhů chyb. Proto ukážeme napřed na jednoduchých případech zjednodušené vzorce a to v klasickém zápise. Výchozí vztah pro úpravu bude vzorec:
kde kromě známých symbolů vyjadřuje Případ konstantní chyby
Korelaci ve skupině měření, kde
Střední chyba Při současném působení náhodných chyb i systematické chyby je třeba odděleně vypočítat úhrnný vliv každé složky na funkci měřených veličin a pak teprve je kvadraticky sečíst, abychom dostali úplnou střední chybu funkce.
Při působení systematické chyby roste u součtu měřených veličin střední chyba rychleji než s odmocninou z počtu veličin. U mnoha veličin může účinek malé systematické chyby převýšit vliv i větší náhodné střední chyby.
Přitom střední chyba jednoho měření Při působení systematické chyby neklesá střední chyba průměru s odmocninou počtu opakovaných měření (takto klesne jen vliv náhodné složky). Případ skupinové chyby
Mějme velký soubor
V základním smíšeném souboru všech hodnot
Úplná chyba a úplná variance (čtverec úplné střední chyby):
V případě stejně velikých skupin
Zejména nyní je zřejmé, jak se každý druh chyb hromadí podle jiného zákona. Klasický zákon přenášení středních chyb platí jen pro náhodnou složku (
a v případě stejně velikých skupin
V aritmetickém průměru klesá vliv střední kvadratické chyby náhodné s odmocninou počtu všech měření (
V případě nestejných vah
a v rovnicích je třeba nahradit Při působení systematické chyby, stálé ve všech skupinách, neklesne střední kvadratická chyba celkového průměru s odmocninou počtu skupin a nelze pro určení střední chyby součtu kvadraticky sčítat střední chyby jednotlivých skupinových výsledků.
V případě současného působení vzájemně nezávislých systematických chyb různého druhu
a střední chyba průměru při stejně velkých skupinách u každého druhu skupinové chyby:
Na závěr ukážeme vztah pro obecný funkční vztah
kde
podle počtu různých
Platí:
Jak je vidět, zapsání univerzálně platného vzorce je pracné a nepřehledné. Proto je vhodnější používat zjednodušeného zákona hromadění úplných chyb napsaného pro každou konkrétní situaci, jak bylo ukázáno výše.
« 10. Zákon hromadění středních chyb |
![Equation $$
{\overline{m}}^2_F=\left[f^2\cdot {\overline{m}}^2\right]+2\cdot \sum{\sum{f_i\cdot f_k\cdot {\overline{m}}_{ik}}},
$$](/wiki/lib/exe/fetch.php?media=wiki:latex:/imgb129820e196442ca3ede7fb362a1be3c.png)
 kovarianci (závislost) veličin
kovarianci (závislost) veličin  a
a  .
.
 , působí pouze neznámá konstantní chyba
, působí pouze neznámá konstantní chyba  , takže platí:
, takže platí: 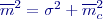 ,
,  a výsledný vztah pak
a výsledný vztah pak
![Equation $$
{\overline{m}}^2_F=\left[f^2\cdot {\sigma }^2\right]+\left[f^2\cdot {\overline{m}}^2_c\right]+2\cdot \sum{\sum{f_i\cdot f_k\cdot }}{\overline{m}}^2_c=\left[f^2\cdot {\sigma }^2\right]+{\left[f\right]}^2\cdot {\overline{m}}^2_c.
$$](/wiki/lib/exe/fetch.php?media=wiki:latex:/img1edd647de53a54d3a94a0bc0b3175f79.png)
 reprezentuje základní soubor všech možných hodnot systematické chyby v různých skupinách (konstantní hodnotu má jen v dané skupině).
reprezentuje základní soubor všech možných hodnot systematické chyby v různých skupinách (konstantní hodnotu má jen v dané skupině).

![Equation $$
{\varepsilon }_S{\rm =}\left[\varepsilon \right]{\rm =}\left[\triangle \right]{\rm +}n\cdot c ,$$](/wiki/lib/exe/fetch.php?media=wiki:latex:/img878d53d2e412d6daa1b59a632139c0a8.png)
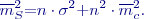

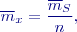
![Equation $$
{\varepsilon }_x{\rm =}\frac{\left[\varepsilon \right]}{n}{\rm =}\frac{\left[\triangle \right]}{n}{\rm +}c ,
$$](/wiki/lib/exe/fetch.php?media=wiki:latex:/imgf3a21b45b17908001bcc1ffc4941b1ea.png)
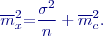
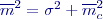 , takže
, takže  .
.
 opakovaných měření nebo chyb, který rozdělíme na
opakovaných měření nebo chyb, který rozdělíme na ,
,  , …,
, …,  počty v jednotlivých skupinách,
počty v jednotlivých skupinách, ![Math $[n]=N$](/wiki/lib/exe/fetch.php?media=wiki:latex:/imgcaf7c9a560b219c37648b08bb6b2e392.png) ,
,
 ,
, ![Math $[p]=1$](/wiki/lib/exe/fetch.php?media=wiki:latex:/img6ed35660751b1e55ed351b81fbaf0a21.png) relativní četnost v
relativní četnost v  ,
,  ,…,
,…,  náhodné chyby, proměnlivé od měření k měření, vzájemně
náhodné chyby, proměnlivé od měření k měření, vzájemně  ,
, 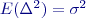 nezávislé a působící rozptyl jednotlivých měření,
nezávislé a působící rozptyl jednotlivých měření,
 ,
,  , …,
, …,  skupinové systematické chyby (nebo jejich průměrné hodnoty), zatěžující stejnou hodnotou všechna měření uvnitř skupiny, ale proměnlivé od skupiny ke skupině (
skupinové systematické chyby (nebo jejich průměrné hodnoty), zatěžující stejnou hodnotou všechna měření uvnitř skupiny, ale proměnlivé od skupiny ke skupině ( ),
), ![Math $\overline{c}=\left[p_i\cdot c_i\right]$](/wiki/lib/exe/fetch.php?media=wiki:latex:/imgf38b765076adc9abf10e503c7d0d0f56.png) jejich průměrná hodnota jakoby utajená konstantní chyba pro všechny skupiny (pro všechna možná měření),
jejich průměrná hodnota jakoby utajená konstantní chyba pro všechny skupiny (pro všechna možná měření),
![Math ${\gamma }_i=c_i-\overline{c},\ \left[p\gamma \right]=0$](/wiki/lib/exe/fetch.php?media=wiki:latex:/imgad88d2d2c93767a3bf42e1204a560865.png) redukované skupinové chyby, stálé a utajené uvnitř skupiny, ale proměnlivé od skupiny ke skupině a ovlivňující rozdíly mezi skupinovými průměry. Mají charakter opravy průměru (
redukované skupinové chyby, stálé a utajené uvnitř skupiny, ale proměnlivé od skupiny ke skupině a ovlivňující rozdíly mezi skupinovými průměry. Mají charakter opravy průměru (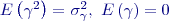 ).
).
 ,
, 


![Math $S=[l]$](/wiki/lib/exe/fetch.php?media=wiki:latex:/img814569b9c242314c7df239172dfb7c40.png) bude skutečná a střední chyba
bude skutečná a střední chyba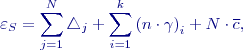
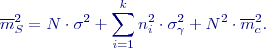
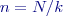 ,
, ![Math $[n^2]=N^2/k$](/wiki/lib/exe/fetch.php?media=wiki:latex:/imga2be3d19bffec2818e2741d7fa1e6c36.png) :
:
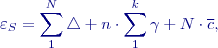
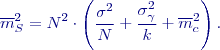
 ).
).
![Equation $$
\overline{x}=\frac{\left[l\right]}{N} , {\varepsilon }_{\overline{x}}=\frac{{\varepsilon }_S}{N} , {\overline{m}}^2_{\overline{x}}=\frac{{\overline{m}}^2_S}{N^2} .
$$](/wiki/lib/exe/fetch.php?media=wiki:latex:/img23cac04239d766178ee501d126cc1785.png)
![Equation $$
{\varepsilon }_{\overline{x}}=\frac{\left[\triangle \right]}{N}+\frac{\left[n\cdot \gamma \right]}{N}+\overline{c},{\overline{m}}^2_x=\frac{{\sigma }^2}{N}+\frac{\left[n^2\right]}{N^2}\cdot {\sigma }^2_{\gamma }+{\overline{m}}^{{\rm 2}}_c .
$$](/wiki/lib/exe/fetch.php?media=wiki:latex:/imga646728873bbd58ac92e38e8c134d051.png)
![Equation $$
{\varepsilon }_{\overline{x}}=\frac{\left[\triangle \right]}{N}+\frac{\left[\gamma \right]}{k}+\overline{c} , {\overline{m}}^2_x=\frac{{\sigma }^2}{N}+\frac{{\sigma }^2_{\gamma }}{k}+\overline{c}, {\overline{m}}^2_x=\frac{{\sigma }^2}{N}+\frac{{\sigma }^2_{\gamma }}{k}+{\overline{m}}^{{\rm 2}}_c .
$$](/wiki/lib/exe/fetch.php?media=wiki:latex:/img1a5770a5d606809438492a48695f03b4.png)
 ), vliv střední proměnlivé systematické chyby skupinové s odmocninou počtu skupin se změněnými podmínkami, vliv konstantní chyby se nezmenší vůbec. Je třeba vypočítat napřed odděleně úhrnný vliv každého druhu chyb a pak je teprve kvadraticky sečíst. Je žádoucí vystřídat co nejvíce podmínky měření, aby konstantní složka chyb
), vliv střední proměnlivé systematické chyby skupinové s odmocninou počtu skupin se změněnými podmínkami, vliv konstantní chyby se nezmenší vůbec. Je třeba vypočítat napřed odděleně úhrnný vliv každého druhu chyb a pak je teprve kvadraticky sečíst. Je žádoucí vystřídat co nejvíce podmínky měření, aby konstantní složka chyb ![Math $x_i={\left[l\right]}_i/n_i$](/wiki/lib/exe/fetch.php?media=wiki:latex:/img736a48d727d7f0a9ac6c8077e32f729d.png) při
při 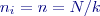
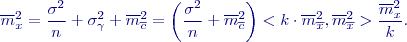
 měření
měření  bude skupinový a celkový průměr
bude skupinový a celkový průměr
![Equation $$
x_i=\frac{{\left[pl\right]}_i}{{\left[p\right]}_i} , \overline{x}=\frac{\left[pl\right]}{\left[p\right]}=\frac{\left[Px\right]}{\left[P\right]} , P_i={\left[p\right]}_i
$$](/wiki/lib/exe/fetch.php?media=wiki:latex:/img7b58db98a74bd5366ca4bc0c40caa95f.png)
![Math $N=[P]$](/wiki/lib/exe/fetch.php?media=wiki:latex:/img97a4732056ac3b199bcc68c500391f81.png) ,
, ![Math $n_i=P_i={\left[p\right]}_i$](/wiki/lib/exe/fetch.php?media=wiki:latex:/img62e8f03c65f6c8631df845c89f70adcc.png) .
.
 ,
,  ,
,  , …,
, …,  platí
platí
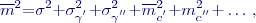
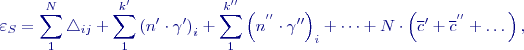
![Equation $$
{\overline{m}}^2_S=N\cdot {\sigma }^2+\left[n^{'2}\right]\cdot {\sigma }^2_{{\gamma }'}+\left[n^{''2}\right]\cdot {\sigma }^2_{{\gamma }^{''}}+\dots +N^2\cdot \left({\overline{m}}^2_{c'}+{\overline{m}}^2_{c^{''}}+\dots \right),
$$](/wiki/lib/exe/fetch.php?media=wiki:latex:/imgec2be55f1106ce678ab55bc3a4ea1f91.png)
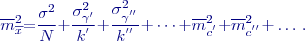
 , kde jsou proměnné závislé. Závislost musí být dána buď kovarianční, nebo korelační maticí. K jejímu určení, či k výpočtu prvku, není obvykle dosti potřebných měření. Je-li závislost způsobena přítomností systematických chyb, musíme znát charakter jejich působení a odhad složek jednotlivých středních chyb. Obecný vztah pak lze upravit a schematicky zapsat:
, kde jsou proměnné závislé. Závislost musí být dána buď kovarianční, nebo korelační maticí. K jejímu určení, či k výpočtu prvku, není obvykle dosti potřebných měření. Je-li závislost způsobena přítomností systematických chyb, musíme znát charakter jejich působení a odhad složek jednotlivých středních chyb. Obecný vztah pak lze upravit a schematicky zapsat:
![Equation $$
m^2_y=\left[{\left(f\cdot m_{\triangle }\right)}^2\right]+\sum{A^2_i\cdot m^2_{\gamma }}+\sum{B^2_i\cdot m^2_{{\gamma }'}}+\dots +{\left[f\cdot m_c\right]}^2,
$$](/wiki/lib/exe/fetch.php?media=wiki:latex:/img25e0f7b8fa2ba73021b0bba7ceec9099.png)
 je střední chyba náhodná, příslušející k proměnné
je střední chyba náhodná, příslušející k proměnné  ; bude-li pro několik proměnných stejná, upraví se prvý člen na řadu
; bude-li pro několik proměnných stejná, upraví se prvý člen na řadu
![Equation $$
{\left[f^2\right]}_1\cdot m^2_{\triangle 1}+{\left[f^2\right]}_2\cdot m^2_{\triangle 2}+\dots
$$](/wiki/lib/exe/fetch.php?media=wiki:latex:/img931a367ec0ad68147ac20a20227a2817.png)
 ;
;  je součet parciálních derivací podle všech proměnných, ve kterých se uplatní stejný druh i velikost proměnlivé systematické chyby
je součet parciálních derivací podle všech proměnných, ve kterých se uplatní stejný druh i velikost proměnlivé systematické chyby  . Indexem
. Indexem  ;
;  totéž pro jiný druh proměnlivé systematické chyby. Stejný druh systematické chyby se rozliší čárkami:
totéž pro jiný druh proměnlivé systematické chyby. Stejný druh systematické chyby se rozliší čárkami:
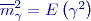 je střední proměnlivá systematická chyba;
je střední proměnlivá systematická chyba;
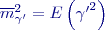 je střední proměnlivá systematická chyba jiného druhu.
je střední proměnlivá systematická chyba jiného druhu.
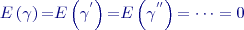 .
.
 jsou různé druhy střední stálé systematické chyby. V případě její konstantní hodnoty pro všechny proměnné se poslední člen upraví na
jsou různé druhy střední stálé systematické chyby. V případě její konstantní hodnoty pro všechny proměnné se poslední člen upraví na ![Math ${\left[f\right]}^2\cdot m^2_{c_0}$](/wiki/lib/exe/fetch.php?media=wiki:latex:/imge29f17fb0b29234d77452605b4058015.png) , kde
, kde 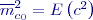 , když písmenem
, když písmenem  označíme náhodnou velikost stálé systematické chyby.
označíme náhodnou velikost stálé systematické chyby.